Unidad 3 Modelo de ANOVA

3.1 Introducción

El modelo de ANOVA se plantea para comparar poblaciones normales, especialmente cuando son más de dos las poblaciones a comparar. Las poblaciones a comparar se identifican a través de una variable clasificadora (de tipo categórico) que actúa como predictora para estimar respuestas medias supuestamente distintas a comparar.

3.2 El modelo de ANOVA

Consideremos una variable respuesta \(Y\) que se distribuye normal, y que viene afectada por una variable de clasificación \(A\) con \(a\) niveles de respuesta distintos (uno por cada una de las poblaciones a comparar). Supongamos que tenemos \(n_i\) observaciones de la respuesta para cada uno de los niveles de respuesta de la variable clasificadora, \(i=1,...,a\). El modelo de ANOVA se plantea asumiendo que en cada nivel o subpoblación, esperamos un valor distinto para la respuesta, \[(y_{ij}|\mu_i,\sigma^2) \sim N(\mu_i,\sigma^2)\] de modo que \[E(y_{ij}|\mu_i,\sigma^2)=\mu_i; \ Var(y_{ij}|\mu_i,\sigma^2)=\sigma^2, \ \ i=1,...,a; \ j=1,...,n_i\] La formulación habitual de este modelo se suele dar en términos de un efecto global y común a todas las observaciones, \(\theta\), y un efecto diferencial respecto del primer nivel del factor de clasificación \(A\), \(\alpha_i\), con los que se construye la media (identificada generalmente por \(\mu\)) o predictor lineal (identificada generalmente por \(\eta\)) y que en el modelo lineal coinciden: \[\mu_{ij}=\eta_{ij}=\theta + \alpha_i\] donde \(\alpha_i=\mu_i-\mu_1\) y \(\mu_1=\theta\), para \(i\geq 1\), esto es, \(\alpha_1=0\).

Estamos pues asumiendo que todos los \(n_i\) sujetos en el subgrupo de población \(i\) identificado por la variable clasificadora \(A\), comparten una media común \(\mu_i\) y cierta variabilidad \(\sigma^2\). Podríamos asumir varianzas distintas para cada subpoblación, pero por simplicidad consideramos que son iguales.

En la modelización bayesiana es preciso añadir distribuciones a priori para cada uno de los parámetros del modelo: los efectos fijos \(\theta,\alpha_i\), y la varianza \(\sigma^2\) de los datos. Ante ausencia de información, se asumirán las distribuciones difusas habituales en INLA:

\[\begin{eqnarray*} (Y_{ij}|\mu_i,\sigma^2) & \sim & N(\mu_i,\sigma^2) \\ && \mu_i = \theta + \alpha_i, i\geq 1 \\ \theta & \sim & N(0,\infty)\\ \alpha_i & \sim & N(0,1000), i\geq 1\\ \tau=1/\sigma^2 & \sim & Ga(1,0.00005) \end{eqnarray*}\]

3.3 Anova de una vía

Vamos a ilustrar el análisis ANOVA en INLA a través de la base de datos coagulation, en la librería faraway, referidos a un estudio de tiempos de coagulación de la sangre en 24 animales a los que aleatoriamente se les asignó una de entre tres dietas distintas (variable clasificadora diet). Posteriormente, para estudiar el efecto de dichas dietas en la coagulación, se tomaron muestras de los tiempos de coagulación (en la variable coag, que es la respuesta).

data(coagulation, package="faraway")
str(coagulation)
#> 'data.frame':    24 obs. of  2 variables:
#>  $ coag: num  62 60 63 59 63 67 71 64 65 66 ...
#>  $ diet: Factor w/ 4 levels "A","B","C","D": 1 1 1 1 2 2 2 2 2 2 ...
ggplot(coagulation,aes(x=diet,y=coag))+
  geom_boxplot(aes(color=diet))+
  theme(legend.position="none")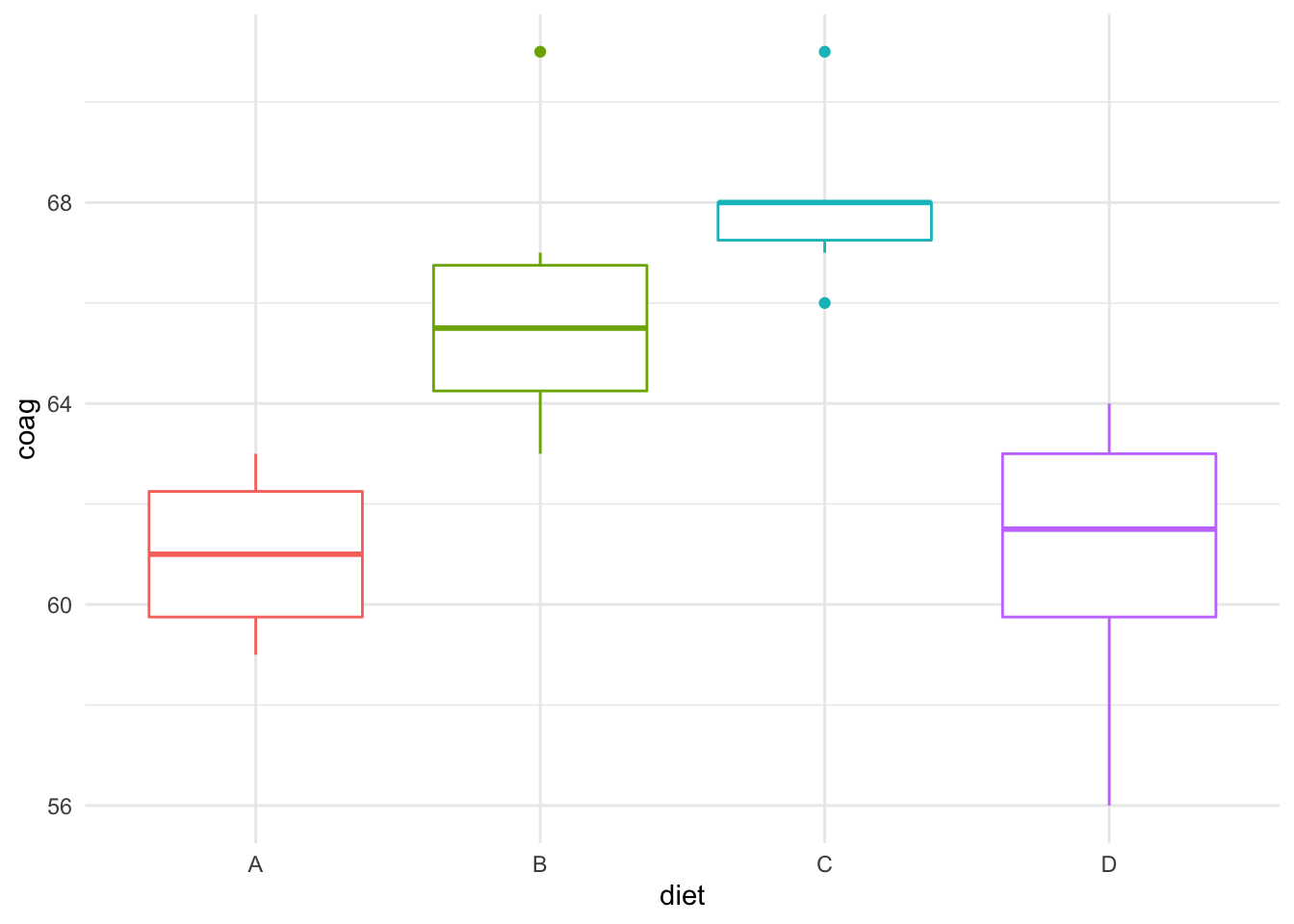

Estamos planteando un modelo de Anova como el propuesto en la sección anterior, donde \(\alpha_i\) identifica el efecto diferencial sobre la respuesta con la dieta A, para el resto de las dietas B y C. Los parámetros del modelo son, como en regresión, los efectos fijos \((\theta,\alpha_i)\) y la varianza \(\sigma^2\), para los que asumimos las priors difusas que por defecto propone INLA. Ajustamos el modelo y obtenemos las inferencias a posteriori

formula=coag ~ diet
fit=inla(formula,family="gaussian",data=coagulation,
         control.compute=list(config=TRUE,return.marginals.predictor=TRUE))
fijos=round(fit$summary.fixed,3);fijos
#>               mean    sd 0.025quant 0.5quant 0.975quant
#> (Intercept) 61.016 1.172     58.700   61.016     63.337
#> dietB        4.979 1.513      1.983    4.980      7.970
#> dietC        6.977 1.513      3.981    6.978      9.968
#> dietD       -0.016 1.435     -2.859   -0.016      2.822
#>             mode kld
#> (Intercept)   NA   0
#> dietB         NA   0
#> dietC         NA   0
#> dietD         NA   0
tau=round(fit$summary.hyperpar,3);tau
#>                                          mean    sd
#> Precision for the Gaussian observations 0.197 0.059
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations      0.099    0.191
#>                                         0.975quant mode
#> Precision for the Gaussian observations      0.328   NA
medias=round(fit$summary.linear.predictor,4)

Atendiendo a los descriptivos de la distribución posterior para los efectos fijos, concluimos:

• El tiempo esperado de coagulación para los animales que han seguido la dieta A es de 61.016(58.7,63.337).
• Los animales que han seguido la dieta B tienen un tiempo de coagulación esperado superior en 4.979 unidades a los de la dieta A, y dicha diferencia es significativamente distinta de cero en el contexto bayesiano, dado que su RC no incluye al cero, (1.983,7.97).
• Una conclusión similar se deriva para la dieta C, que da un tiempo de coagulación esperado superior en 6.977 unidades a los de la dieta A, y una RC (3.981,9.968).
• Las diferencias en los tiempos de coagulación de seguir una dieta D frente a la dieta A no son relevantes. De hecho, la diferencia entre ellos es de -0.016 y el intervalo RC contiene al cero, (-2.859,2.822).

Pintamos a continuación en la Figura 3.1 la distribución posterior de los tiempos esperados de coagulación \(\mu_i\) (o predictores lineales) para cada una de las dietas. En la Figura 3.2 se añaden las medias posteriores y las regiones creíbles.

dietas=levels(coagulation$diet)
pred=NULL
for(i in 1:length(dietas)){
index=which(coagulation$diet==dietas[i])[1]
# distrib. posterior
post=as.data.frame(fit$marginals.fitted.values[[index]])
# media
e=fit$summary.fitted.values[index,1]
rc.low=fit$summary.fitted.values[index,3]
rc.up=fit$summary.fitted.values[index,5]
pred=rbind(pred,data.frame(dieta=dietas[i],
                           post,e,rc.low,rc.up))
}

ggplot(pred, aes(x = x, y =y)) + 
  geom_line(aes(color=dieta))+
  labs(x=expression(paste("Tiempo medio de coagulación:",mu)),
       y="D.Posterior")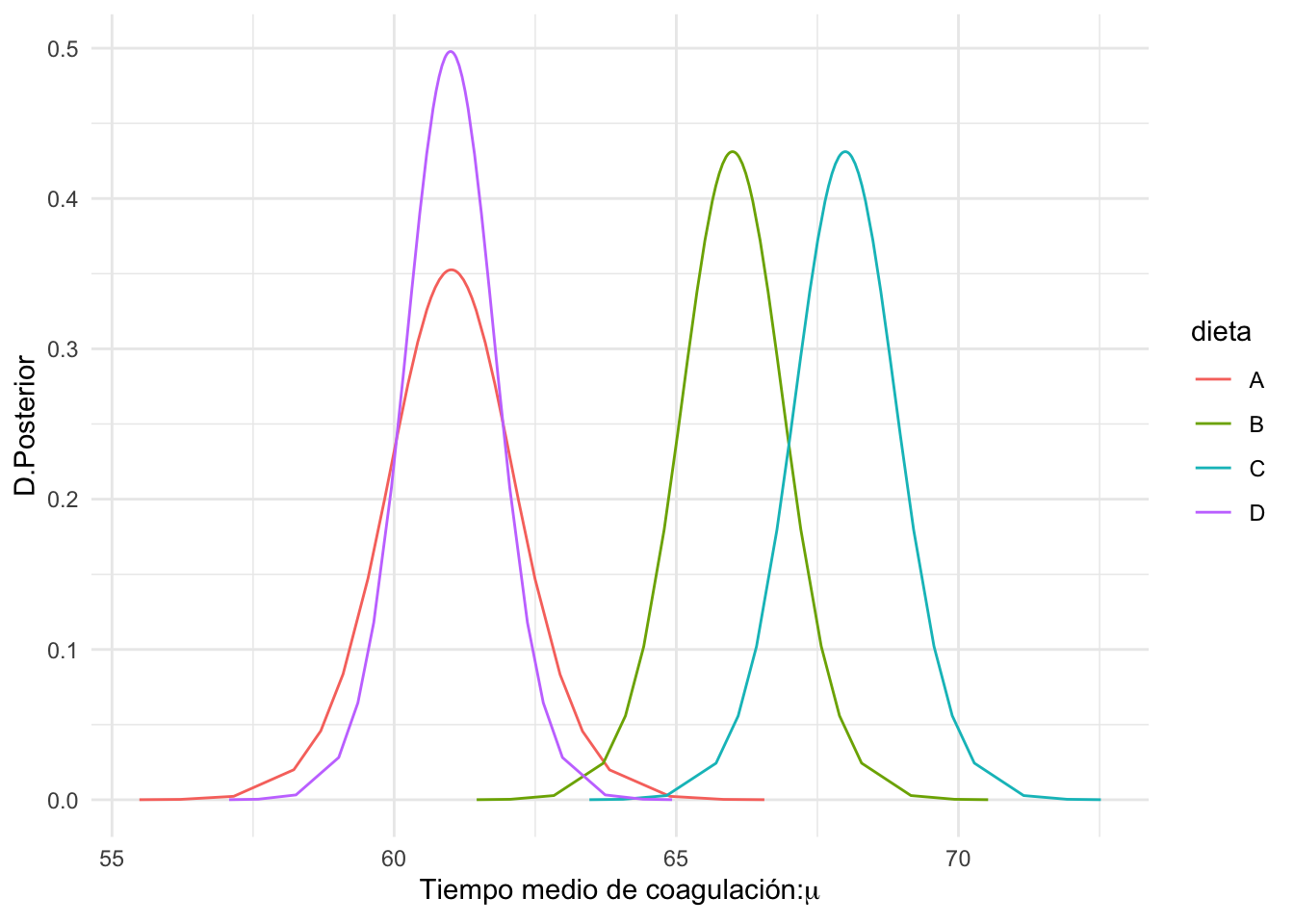

Figura 3.1: Distribución posterior del tiempo medio de coagulación para las 4 dietas.

Podríamos ajustar el modelo prescindiendo del efecto de interceptación y estimar directamente los efectos.

formula=coag ~ -1 + diet
fit=inla(formula,family="gaussian",data=coagulation,
         control.compute=list(config=TRUE,return.marginals.predictor=TRUE))
round(fit$summary.fixed,3)
#>         mean    sd 0.025quant 0.5quant 0.975quant mode kld
#> dietA 60.916 1.176     58.577   60.919     63.233   NA   0
#> dietB 65.939 0.961     64.030   65.942     67.832   NA   0
#> dietC 67.937 0.961     66.028   67.940     69.830   NA   0
#> dietD 60.958 0.832     59.306   60.960     62.599   NA   0
round(fit$summary.hyperpar,3)
#>                                          mean   sd
#> Precision for the Gaussian observations 0.197 0.06
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations      0.098     0.19
#>                                         0.975quant mode
#> Precision for the Gaussian observations      0.324   NA

Con lo cual la representación gráfica se simplifica a través, directamente, de las distribuciones posteriores de los efectos fijos.

pred=NULL
for(i in 1:length(names(fit$marginals.fixed))){
  pred=rbind(pred,data.frame(as.data.frame(fit$marginals.fixed[[i]]),
                  dieta=names(fit$marginals.fixed)[i],
                  mean=fit$summary.fixed$mean[i],
                  rc.low=fit$summary.fixed$'0.025quant'[i],
                  rc.up=fit$summary.fixed$'0.975quant'[i]))}

ggplot(pred, aes(x = x, y =y)) + 
  geom_line(aes(color=dieta))+
  geom_vline(aes(xintercept=mean,color=dieta),linetype="dashed")+
  geom_vline(aes(xintercept=rc.low,color=dieta),linetype="dotted")+
  geom_vline(aes(xintercept=rc.up,color=dieta),linetype="dotted")+
  facet_wrap(vars(dieta))+
  labs(x=expression(paste("Tiempo medio de coagulación:",mu)),
       y="D.Posterior",title="D.Posterior, medias y RC95%")+
  theme(legend.position="none")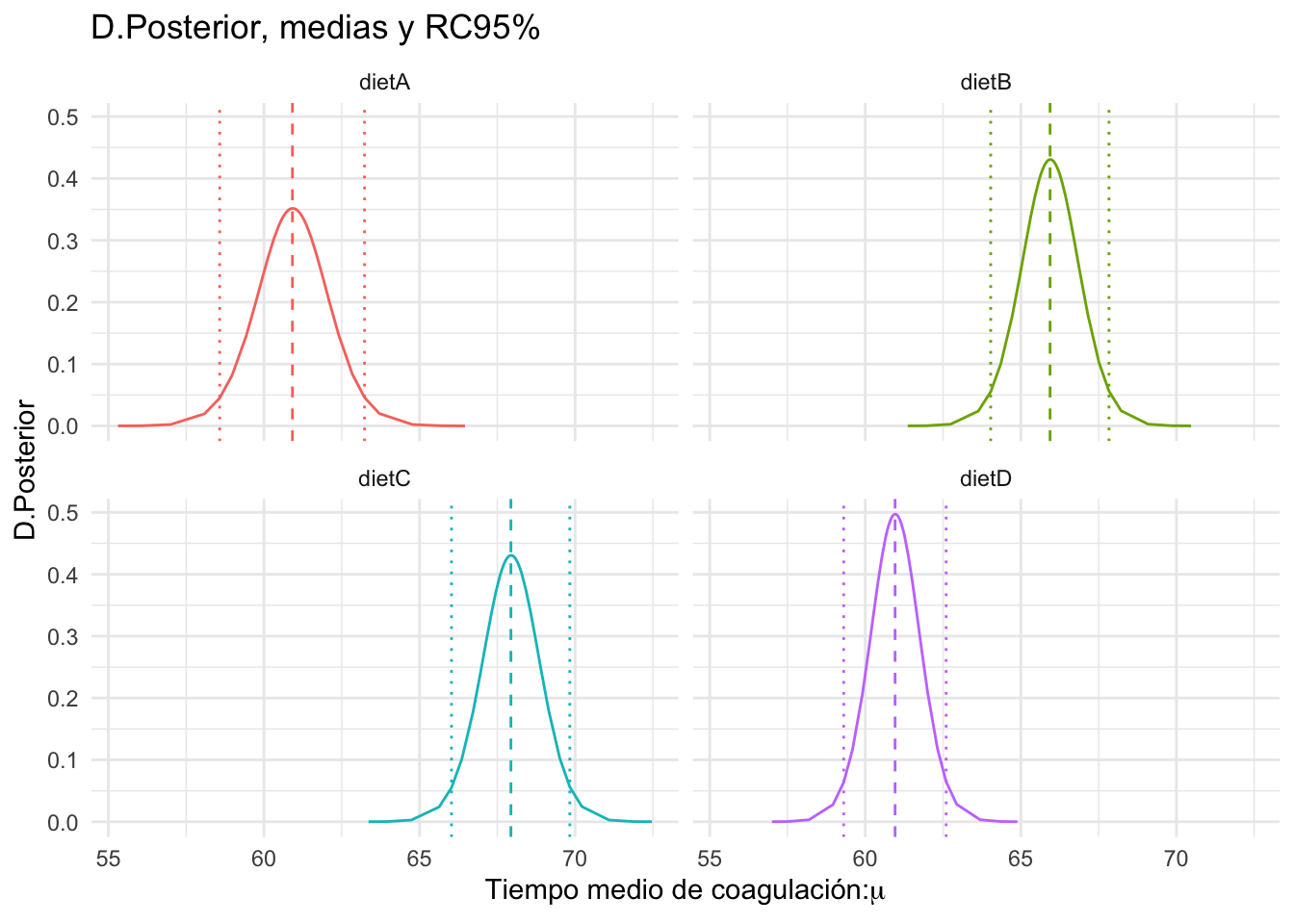

Figura 3.2: Distribuciones posteriores, medias y RC del tiempo esperado de coagulación.

Como ya hacíamos en regresión, podemos inferir sobre la desviación típica de los datos, \(\sigma\), transformando la distribución para la precisión \(\tau\). La distribución posterior junto con su media y RC95% se muestra en la Figura 3.3.

sigma.post=inla.tmarginal(function(tau) tau^(-1/2),
  fit$marginals.hyperpar[[1]])
# y la pintamos
ggplot(as.data.frame(sigma.post)) + 
  geom_line(aes(x = x, y = y)) +
  labs(x=expression(sigma),y="D.Posterior")+
  geom_vline(xintercept=inla.hpdmarginal(0.95,sigma.post),
             linetype="dotted",color="blue")+
  geom_vline(xintercept=inla.emarginal(function(x) x,sigma.post),
             linetype="dashed",color="blue")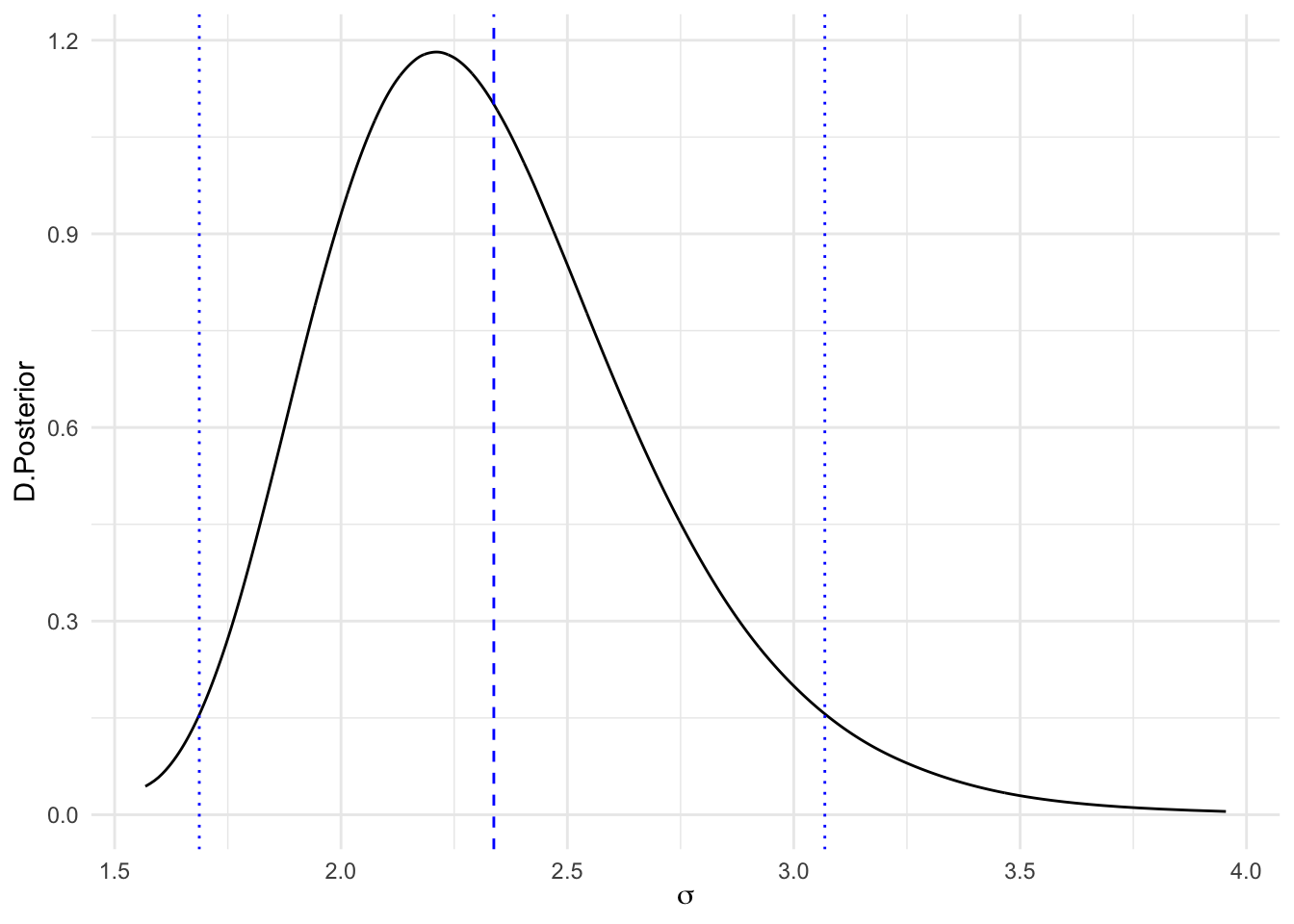

Figura 3.3: Distribución posterior, media y RC, de la desviación típica de los datos (sigma)

# Valor esperado
sigma.e=round(inla.emarginal(function(tau) tau^(-1/2),
  fit$marginals.hyperpar[[1]]),4)
# HPD95%
sigma.hpd=round(inla.hpdmarginal(0.95,sigma.post),3)
paste("E(sigma.post)=",sigma.e,"HPD95%=(",sigma.hpd[1],",",sigma.hpd[2],")")
#> [1] "E(sigma.post)= 2.3379 HPD95%=( 1.687 , 3.069 )"

Si queremos inferir sobre la diferencia entre cualesquiera de los efectos podemos recurrir a simular la distribución posterior de las diferencias. Por ejemplo, supongamos que queremos comparar la dieta B con la dieta C. Simulamos entonces de las distribuciones posteriores de \(\mu_B\) y de \(\mu_C\), y obtenemos la diferencia \(\mu_B-\mu_C\).

\[ \mu_B^{(i)} \sim \pi(\mu_B|y), \ \mu_C^{(i)} \sim \pi(\mu_C|y) \Rightarrow \mu_C^{(i)}-\mu_B^{(i)} \sim \pi(\mu_C-\mu_B|y), \ \ i=1,\ldots,nsim\]

sims=inla.posterior.sample(1000,fit,selection=list(dietB=1,dietC=1))
dif_CB=as.vector(inla.posterior.sample.eval(function(...) dietC-dietB, sims))
pred=data.frame(dif=dif_CB)
ggplot(pred,aes(x=dif))+
  geom_histogram(aes(y=..density..), colour="black", fill="white")+
 geom_density(alpha=.2, fill="#80E7F5")+
  geom_vline(xintercept=mean(dif_CB),color="red",size=1.5)+
  geom_vline(xintercept=quantile(dif_CB,probs=c(0.025,0.975)),color="red",size=1.5,linetype="dashed")+
  labs(x="Diferencia del tiempo esperado de coagulación: dietC-dietB",y="")
#> `stat_bin()` using `bins = 30`. Pick better value with
#> `binwidth`.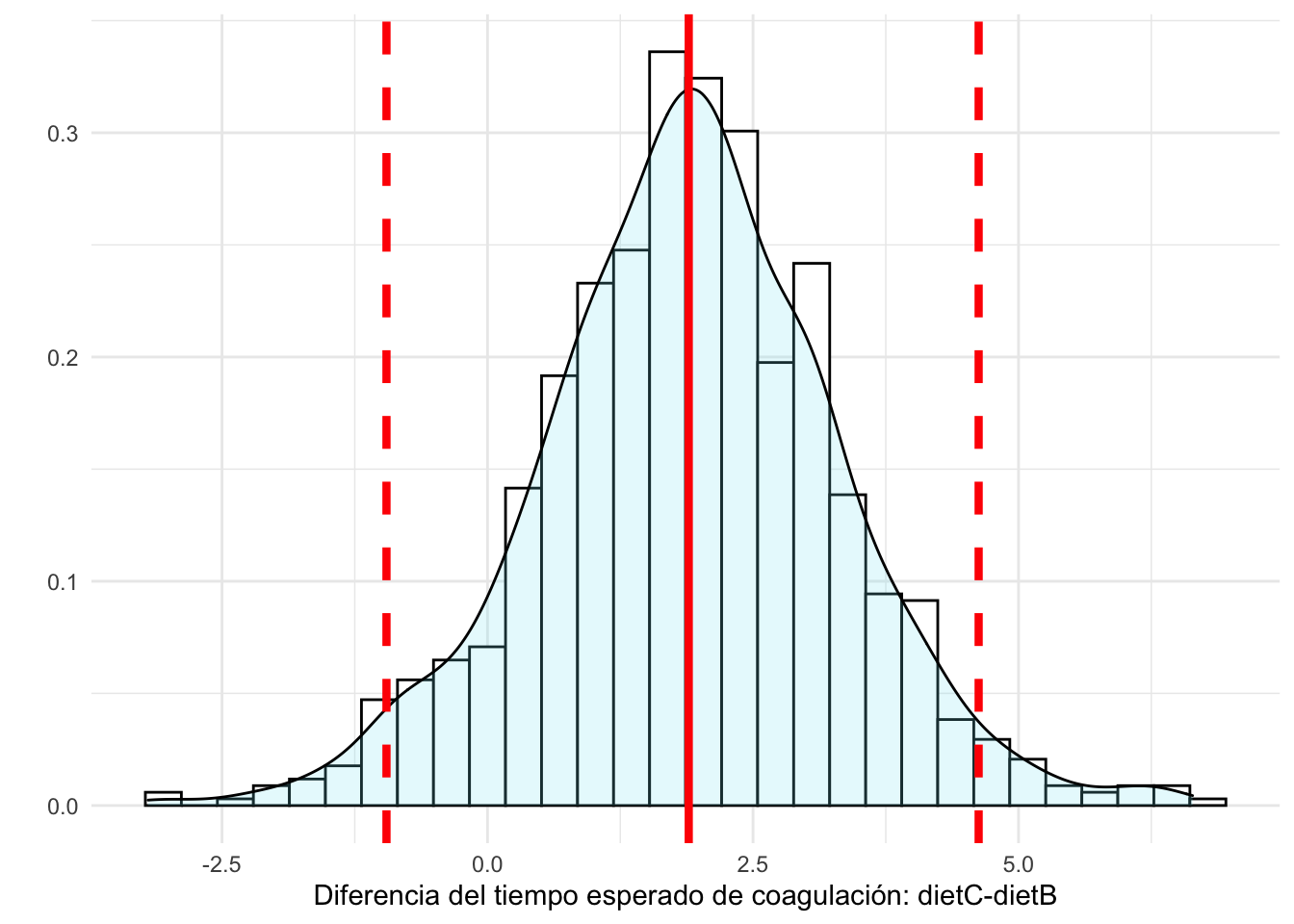

Podríamos así mismo, calcular cualquier probabilidad con ellas, como por ejemplo la probabilidad de que el tiempo de coagulación de un animal que sigue la dieta C sea 2 unidades superior al de uno que sigue la dieta B.

\[Pr(\mu_C>\mu_B+2|y)= Pr(\mu_C-\mu_B>2|y)\]

cat(paste("Probabilidad posterior de que muC>muB+2 =",mean(pred$dif>2)))
#> Probabilidad posterior de que muC>muB+2 = 0.464

3.4 Anova de varias vías

Generalmente, y en especial cuando trabajamos con experimentación, son varios los factores que controlamos para investigar el efecto que producen en una respuesta continua. Hablamos de modelos de Anova de varias vías.

Utilizamos la base de datos butterfat en la librería faraway para ilustrar el ajuste con INLA de un modelo de Anova de varias vías. Esta base de datos contiene 100 registros del contenido en grasa láctea, Butterfat, para muestras aleatorias de 20 vacas (10 de ellas de 2 años y 10 maduras, con más de 4 años -en la variable Age) de cada una de cinco razas (en la variable Breed).

El objetivo es investigar las diferencias en materia grasa entre razas y edad, con el fin último de identificar cuáles producen más materia grasa y cuáles menos. Veamos los datos en la Figura 3.4.

data(butterfat,package="faraway")
str(butterfat)
#> 'data.frame':    100 obs. of  3 variables:
#>  $ Butterfat: num  3.74 4.01 3.77 3.78 4.1 4.06 4.27 3.94 4.11 4.25 ...
#>  $ Breed    : Factor w/ 5 levels "Ayrshire","Canadian",..: 1 1 1 1 1 1 1 1 1 1 ...
#>  $ Age      : Factor w/ 2 levels "2year","Mature": 2 1 2 1 2 1 2 1 2 1 ...
ggplot(butterfat,aes(x=Breed,y=Butterfat))+
  geom_boxplot(aes(color=Age))+
  coord_flip()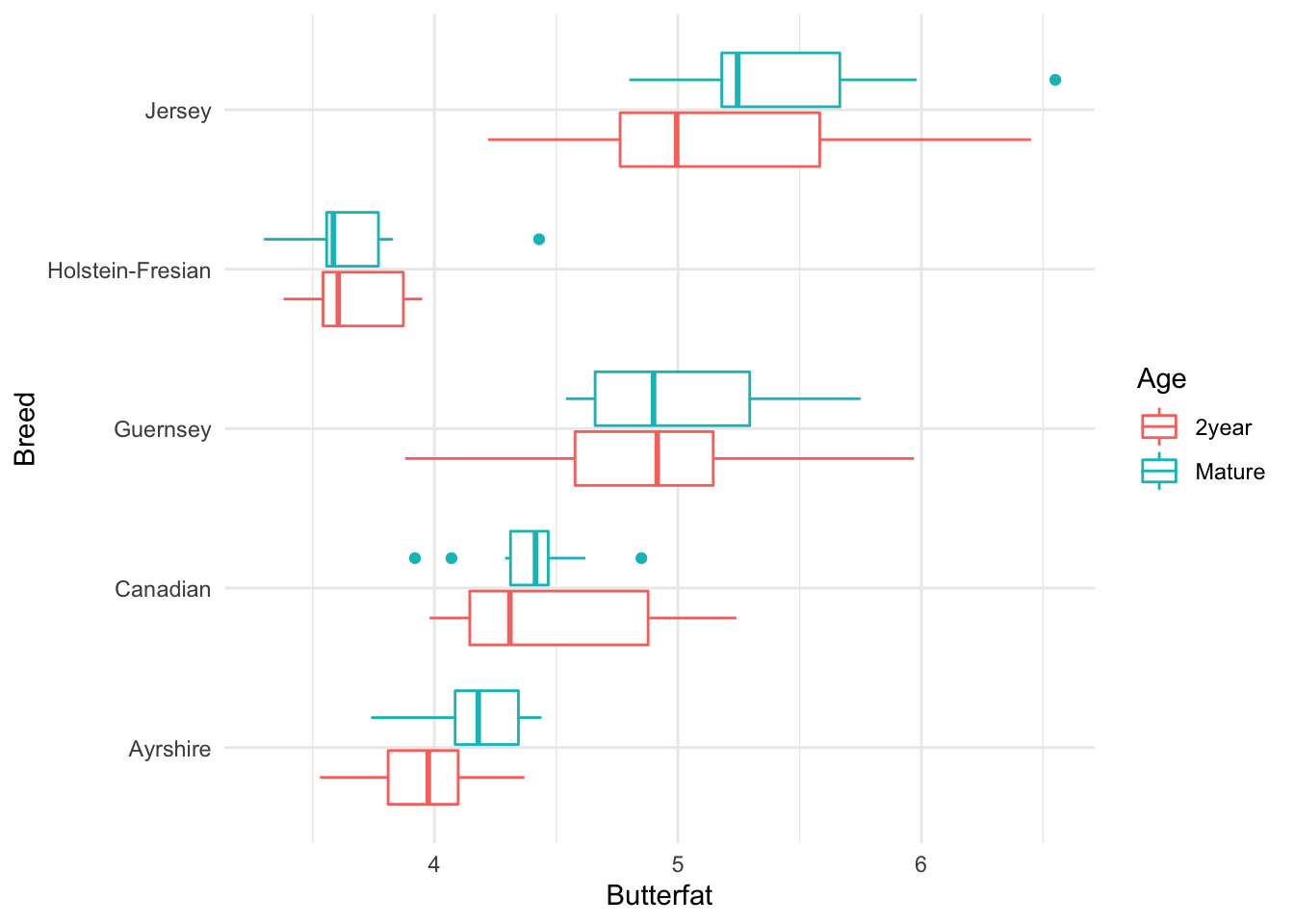

Figura 3.4: Base de datos butterfat, en la librería Faraway

A la vista del gráfico, apreciamos que por lo general, en la mayoría de las razas, las vacas más jóvenes tienen menor contenido en materia grasa que las más viejas. Sin embargo, tal afirmación no parece tan clara en las razas Guernsey y Holstein-Fresian, de modo que para modelizar nuestros datos vamos a considerar a priori, la posibilidad de interacciones entre los factores de clasificación Breed y Age.

Cuando nos enfrentamos a varios factores de clasificación, cabe la posibilidad de que interaccionen entre ellos, esto es, que en algunos niveles de un factor actúen de forma diferente a los otros cuando se combinan con los niveles de algún otro factor. El orden de una interacción viene dado por el número de factores de clasificación que involucra, de modo que hablamos de interacciones de orden 2 si consideramos la interacción entre dos factores, de orden 3 si consideramos la interacción entre tres factores, etc. Generalmente trabajamos con interacciones de orden bajo, dada la complejidad de las conclusiones en interacciones de orden alto. Por otro lado, siempre es importante tener en cuenta de cuántos datos disponemos para conocer a priori la posibilidad de estimar con fiabilidad los distintos efectos de interacción: una interacción de dos factores con \(n_1\) y \(n_2\) niveles de clasificación respectivamente, revierte en la estimación de \((n_1-1)\times(n_2-1)\) efectos de interacción adicionales.

Así, en nuestro problema si estamos planteando la posibilidad de que haya interacciones entre los dos factores de clasificación, estamos asumiendo un modelo de tipo siguiente, asumiendo normalidad en la respuesta:

\[(y_{ijk}|\mu_{ij},\sigma^2) \sim N(\mu_{ij},\sigma^2)\] con \[\mu_{ij}=\theta+ \alpha_i + \beta_j + \alpha\beta_{ij}\] donde en nuestro ejemplo, \(\alpha_i\) es el efecto diferencial (respecto del primer nivel) que aporta el nivel \(i\) de la variable Breed, \(\beta_j\) el efecto asociado a la variable Age, y \(\alpha\beta\) la correspondiente interacción entre ellas. En R una interacción de orden 2 entre dos variables \(f_1\) y \(f_2\) se especifica con \(f_1:f_2\); los efectos principales y la interacción se pueden especificar de varios modos alternativos: \[f_1+f_2+f_1:f_2 \equiv f_1*f_2 \equiv (f_1+f_2)\hat{} 2\]

Veamos cómo ajustar con INLA este modelo, recabando también los criterios de selección DIC y WAIC.

formula=Butterfat ~ Breed * Age
fit=inla(formula,data=butterfat,
         control.compute=list(dic = TRUE, waic = TRUE))
round(fit$summary.fixed,3)
#>                                   mean    sd 0.025quant
#> (Intercept)                      3.966 0.131      3.708
#> BreedCanadian                    0.522 0.186      0.157
#> BreedGuernsey                    0.933 0.186      0.568
#> BreedHolstein-Fresian           -0.303 0.186     -0.668
#> BreedJersey                      1.167 0.186      0.802
#> AgeMature                        0.188 0.186     -0.177
#> BreedCanadian:AgeMature         -0.287 0.263     -0.804
#> BreedGuernsey:AgeMature         -0.086 0.263     -0.603
#> BreedHolstein-Fresian:AgeMature -0.175 0.263     -0.692
#> BreedJersey:AgeMature            0.131 0.263     -0.386
#>                                 0.5quant 0.975quant mode
#> (Intercept)                        3.966      4.224   NA
#> BreedCanadian                      0.522      0.887   NA
#> BreedGuernsey                      0.933      1.298   NA
#> BreedHolstein-Fresian             -0.303      0.062   NA
#> BreedJersey                        1.167      1.532   NA
#> AgeMature                          0.188      0.553   NA
#> BreedCanadian:AgeMature           -0.287      0.230   NA
#> BreedGuernsey:AgeMature           -0.086      0.431   NA
#> BreedHolstein-Fresian:AgeMature   -0.175      0.342   NA
#> BreedJersey:AgeMature              0.131      0.648   NA
#>                                 kld
#> (Intercept)                       0
#> BreedCanadian                     0
#> BreedGuernsey                     0
#> BreedHolstein-Fresian             0
#> BreedJersey                       0
#> AgeMature                         0
#> BreedCanadian:AgeMature           0
#> BreedGuernsey:AgeMature           0
#> BreedHolstein-Fresian:AgeMature   0
#> BreedJersey:AgeMature             0
fit$dic$dic
#> [1] 120.486
fit$waic$waic
#> [1] 121.7376

Observamos en la inferencia posterior para los efectos fijos, que todas las RC asociadas a los efectos de interacción contienen al cero, lo que descarta la relevancia de la interacción a la hora de predecir la respuesta. Reajustamos pues el modelo eliminando la interacción, y comprobamos que efectivamente al eliminarla conseguimos reducir los valores del DIC y WAIC que usamos habitualmente para la selección de variables.

formula=Butterfat ~ Breed + Age
fit=inla(formula,data=butterfat,
         control.predictor=list(compute=TRUE),
         control.compute=list(return.marginals.predictor=TRUE,
                              dic = TRUE, waic = TRUE))
fit$summary.fixed
#>                             mean         sd  0.025quant
#> (Intercept)            4.0077184 0.10124736  3.80873953
#> BreedCanadian          0.3784787 0.13070976  0.12159688
#> BreedGuernsey          0.8899744 0.13070976  0.63309239
#> BreedHolstein-Fresian -0.3905147 0.13070976 -0.64739636
#> BreedJersey            1.2324714 0.13070976  0.97558938
#> AgeMature              0.1045993 0.08266909 -0.05786863
#>                         0.5quant 0.975quant mode
#> (Intercept)            4.0077182  4.2066983   NA
#> BreedCanadian          0.3784790  0.6353594   NA
#> BreedGuernsey          0.8899746  1.1468549   NA
#> BreedHolstein-Fresian -0.3905145 -0.1336339   NA
#> BreedJersey            1.2324717  1.4893519   NA
#> AgeMature              0.1045993  0.2670672   NA
#>                                kld
#> (Intercept)           2.522907e-09
#> BreedCanadian         2.522866e-09
#> BreedGuernsey         2.522869e-09
#> BreedHolstein-Fresian 2.522867e-09
#> BreedJersey           2.522861e-09
#> AgeMature             2.523098e-09
fit$waic$waic
#> [1] 116.3439
fit$dic$dic
#> [1] 115.3833

Observamos ya a partir del modelo ajustado, que el efecto de la edad no es relevante (su RC incluye al cero), pero sin embargo sí que hay diferencias debido a las razas.

Reajustamos de nuevo el modelo, excluyendo la variable Age, y verificamos la reducción (ligera) del DIC/WAIC, lo cual justifica usar este modelo para la predicción.

formula=Butterfat ~ Breed 
fit=inla(formula,data=butterfat,
         control.predictor=list(compute=TRUE),
         control.compute=list(return.marginals.predictor=TRUE,
                              dic = TRUE, waic = TRUE))
fit$summary.fixed
#>                             mean         sd 0.025quant
#> (Intercept)            4.0600181 0.09271795  3.8778058
#> BreedCanadian          0.3784786 0.13112327  0.1207895
#> BreedGuernsey          0.8899742 0.13112327  0.6322850
#> BreedHolstein-Fresian -0.3905148 0.13112327 -0.6482037
#> BreedJersey            1.2324713 0.13112327  0.9747820
#>                         0.5quant 0.975quant mode
#> (Intercept)            4.0600180  4.2422315   NA
#> BreedCanadian          0.3784788  0.6361665   NA
#> BreedGuernsey          0.8899745  1.1476619   NA
#> BreedHolstein-Fresian -0.3905146 -0.1328267   NA
#> BreedJersey            1.2324715  1.4901589   NA
#>                                kld
#> (Intercept)           2.473640e-09
#> BreedCanadian         2.473448e-09
#> BreedGuernsey         2.473453e-09
#> BreedHolstein-Fresian 2.473450e-09
#> BreedJersey           2.473442e-09
fit$waic$waic
#> [1] 115.9279
fit$dic$dic
#> [1] 115.0075

Procederíamos igual que en el modelo de Anova de una vía para la representación de las distribuciones posteriores sobre las medias o predictores lineales en cada una de las razas. Igualmente representaremos la distribución posterior del parámetro de dispersión de los datos \(\sigma\).

3.5 Análisis de ANCOVA

En ocasiones tenemos una variable respuesta de tipo numérico, y como posibles predictores, tanto variables de tipo numérico como variables clasificadoras o factores. Surge entonces la posibilidad de que los predictores numéricos afecten a la respuesta de modo distinto en diferentes niveles de clasificación de los factores; hablamos entonces de interacción entre covariables y factores. Veamos un ejemplo para comprender cómo funcionan estos modelos y cómo se ajustan con INLA.

Consideramos los datos de Galton sobre la regresión de las alturas de los hijos sobre la de los padres (Fte: Galton’s Height Data). Tenemos la estatura del padre, de la madre y del hijo/a, identificado/a por su sexo. Vamos a formular un modelo de regresión de la estatura de los hijos en función de la de sus padres y su género.

url="https://raw.githubusercontent.com/BayesModel/data/main/Galton.txt"
datos<-read.csv(file=url,header=TRUE,dec=".", sep="")
str(datos)
#> 'data.frame':    898 obs. of  6 variables:
#>  $ Family: chr  "1" "1" "1" "1" ...
#>  $ Father: num  78.5 78.5 78.5 78.5 75.5 75.5 75.5 75.5 75 75 ...
#>  $ Mother: num  67 67 67 67 66.5 66.5 66.5 66.5 64 64 ...
#>  $ Gender: chr  "M" "F" "F" "F" ...
#>  $ Height: num  73.2 69.2 69 69 73.5 72.5 65.5 65.5 71 68 ...
#>  $ Kids  : int  4 4 4 4 4 4 4 4 2 2 ...
datos %>% 
  pivot_longer(cols=c("Father","Mother"),
               names_to = "Parents",values_to="Height_parents") %>%
  ggplot(aes(x=Height_parents,y=Height))+
  geom_point(aes(color=Gender))+
  geom_smooth(method="lm",aes(color=Gender),se=FALSE)+
  facet_wrap(vars(Parents))+
  labs(x="Estatura de los padres",y="Estatura de los hijos")
#> `geom_smooth()` using formula 'y ~ x'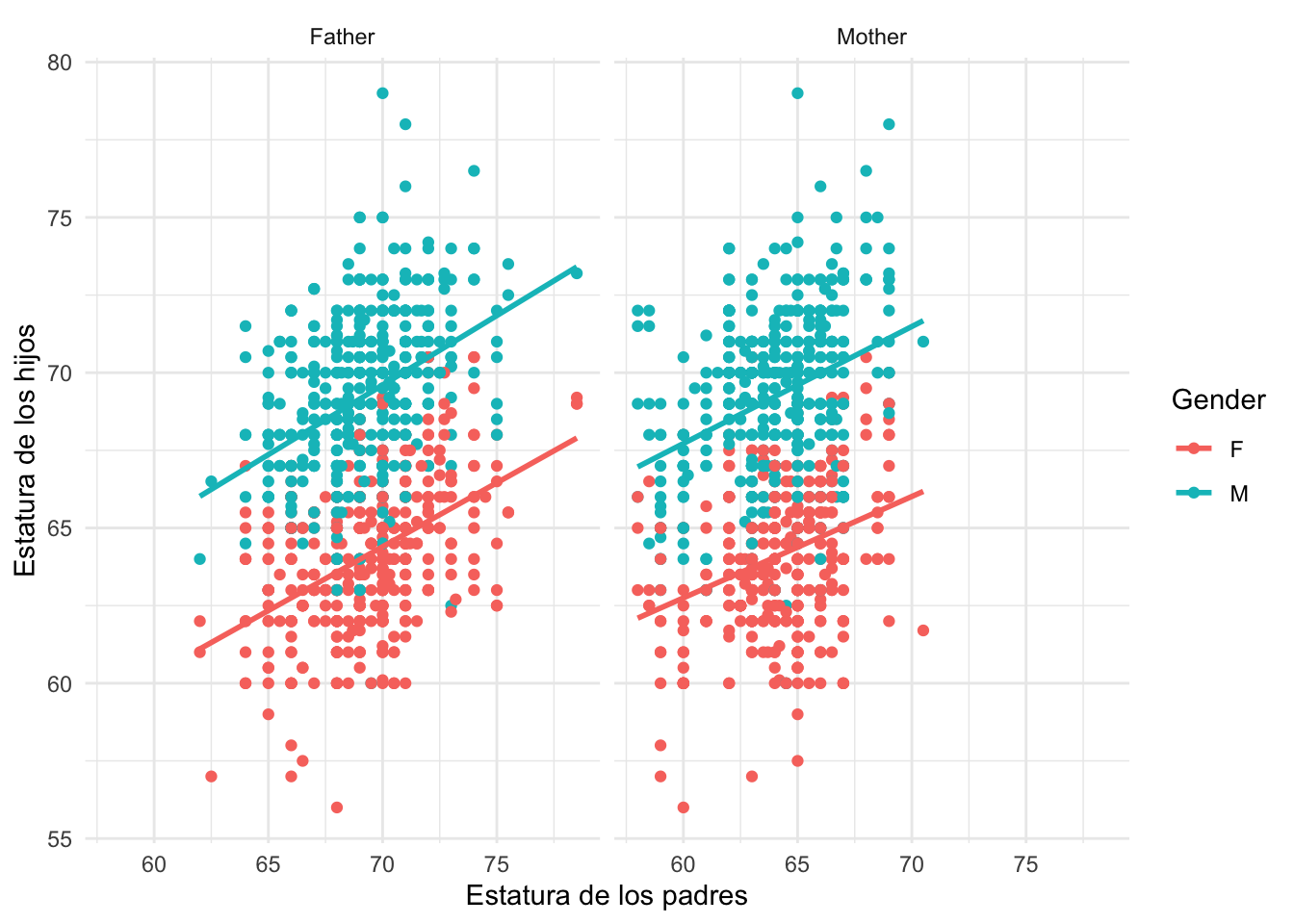

Asumimos pues como respuesta la variable y=Height, como regresores las variables \(x_1=\)Father y \(x_2=\)Mother con las estaturas del padre y la madre respectivamente, y con factor de clasificación la variable \(G=\)Gender, con niveles M/F. En principio cabrían posibles interacciones entre los regresores (estaturas del padre y de la madre) y los factores de clasificación (sexo del sujeto). Esto implicaría que las pendientes de relación ‘estatura padres’ versus ‘estatura hijos’ no serían paralelas para los sujetos hombres y mujeres. Planteamos pues, para predecir la respuesta del sujeto \(j\) en el grupo \(i\) del factor de clasificación (Gender), \(y_{ij}\), el modelo:

\[(y_{ij}|\mu_{ij},\sigma^2) \sim N(\mu_{ij},\sigma^2)\] con el predictor lineal \[\eta_{ij}=\mu_{ij}=\beta_0+ \alpha_M+ (\beta_1 + \beta_1^M) x_{1j} + (\beta_2+ \beta_2^M) x_{2j} ;\ \ j =1,...,n_i; i=M,F\] donde \(\alpha_M\) es el efecto diferencial global de los hombres frente a las mujeres al predecir la estatura, y \(\beta_1^M, \beta_2^M\) son los efectos diferenciales que afectan a los regresores para los sujetos varones, y por lo tanto que provocan pendientes distintas al predecir la estatura del sujeto con las de los padres, en función de si este es hombre o mujer.

Asumimos una distribución vaga sobre todos los efectos fijos y \(\tau=1/\sigma^2\), y ajustamos el modelo Gausiano en INLA:

formula = Height ~ 1+(Father+Mother)*Gender
fit = inla(formula,family = "gaussian",data=datos)
round(fit$summary.fixed,3)
#>                  mean    sd 0.025quant 0.5quant 0.975quant
#> (Intercept)    16.652 3.887      9.027   16.652     24.277
#> Father          0.400 0.039      0.324    0.400      0.477
#> Mother          0.307 0.045      0.218    0.307      0.396
#> GenderM         2.707 5.428     -7.941    2.707     13.354
#> Father:GenderM  0.012 0.058     -0.103    0.012      0.126
#> Mother:GenderM  0.027 0.062     -0.096    0.027      0.149
#>                mode kld
#> (Intercept)      NA   0
#> Father           NA   0
#> Mother           NA   0
#> GenderM          NA   0
#> Father:GenderM   NA   0
#> Mother:GenderM   NA   0

Observamos que ninguna de las interacciones tienen un efecto a considerar (su RC posterior incluye al cero), de modo que las descartamos y reajustamos el modelo sin ellas.

\[\eta_{ij}=\mu_{ij}=\beta_0 + \alpha_M + \beta_1 x_{1j} + \beta_2 x_{2j} ;\ \ j =1,...,n; i=M,F.\]

formula = Height ~ Father+Mother+Gender
fit = inla(formula,family = "gaussian",data=datos,
        control.predictor=list(compute=TRUE),
         control.compute=list(return.marginals.predictor=TRUE,
                              dic = TRUE, waic = TRUE))
round(fit$summary.fixed,3)
#>               mean    sd 0.025quant 0.5quant 0.975quant
#> (Intercept) 15.345 2.746      9.958   15.345     20.733
#> Father       0.406 0.029      0.349    0.406      0.463
#> Mother       0.321 0.031      0.260    0.321      0.383
#> GenderM      5.226 0.144      4.943    5.226      5.508
#>             mode kld
#> (Intercept)   NA   0
#> Father        NA   0
#> Mother        NA   0
#> GenderM       NA   0

Ahora todos los efectos fijos son relevantes para predecir la estatura de los hijos. Utilizamos este modelo para derivar las inferencias.

Representamos a continuación en la Figura 3.5 las distribuciones posteriores de los efectos fijos:

fixed=names(fit$marginals.fixed)
g=list()
for(i in 1:length(fixed)){
  g[[i]]=ggplot(as.data.frame(fit$marginals.fixed[[i]]),aes(x=x,y=y))+
    geom_line()+
    geom_vline(xintercept=fit$summary.fixed$mean[i],linetype="dashed")+
    geom_vline(xintercept=fit$summary.fixed[i,3],linetype="dotted")+
    geom_vline(xintercept=fit$summary.fixed[i,5],linetype="dotted")+
    labs(x=fixed[i],y="D.posterior")
}
grid.arrange(g[[1]],g[[2]],g[[3]],g[[4]],ncol=2)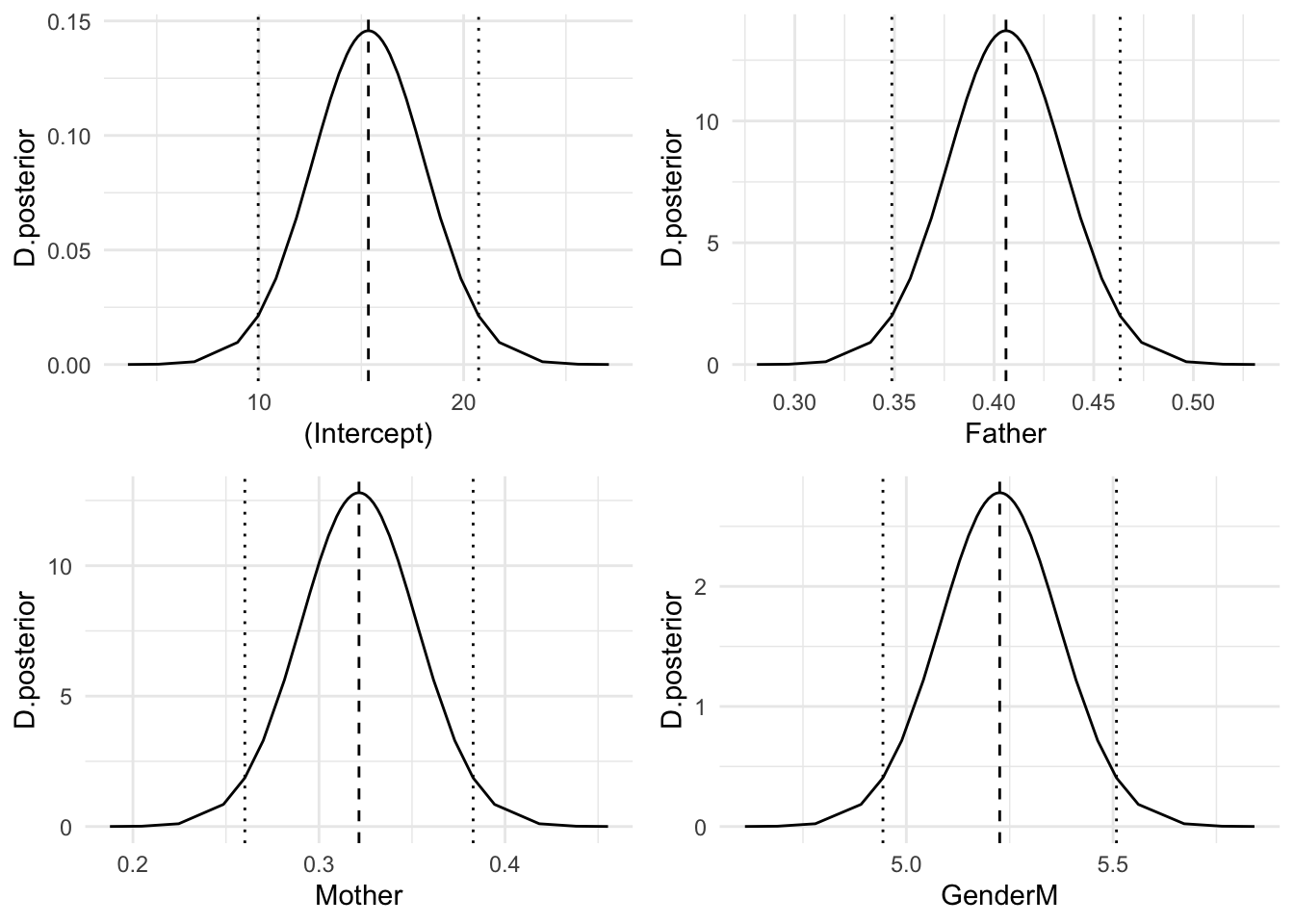

Figura 3.5: Distribución posterior de los efectos fijos

En media observamos que la estatura de los hombres es 5.23 unidades superior a la de las mujeres.

Con estas distribuciones podemos calcular cualquier probabilidad, como por ejemplo,la probabilidad de que la estatura de un hombre supere en 5 unidades a la de una mujer, independientemente de cómo sean sus padres, esto es, \[Pr(\alpha_M>5|datos)\]

1-inla.pmarginal(5,fit$marginals.fixed$"GenderM")
#> [1] 0.9414474

Podemos acceder a las distribuciones posteriores de la estatura de cualquiera de los sujetos en la muestra y posicionar las estaturas de sus padres, que se muestran en la Figura 3.6

# la predicción del predictor lineal para cada sujeto es:
pred<-fit$marginals.linear.predictor
# que en este caso coincide con los valores ajustados
fitted<-fit$marginals.fitted.values
ggplot(as.data.frame(pred$Predictor.1),aes(x=x,y=y))+
  geom_line()+
  labs(x="Estatura media del sujeto 1",y="D.posterior")+
  geom_vline(xintercept=fit$summary.fitted.values$mean[1],linetype="dashed")+
  geom_vline(xintercept=datos$Father[1],linetype="dashed",color="blue")+
  geom_vline(xintercept=datos$Mother[1],linetype="dashed",color="pink")+
  annotate("text",x=datos$Mother[1]+1,y=1,label="Madre")+
  annotate("text",x=datos$Father[1]-1,y=1,label="Padre")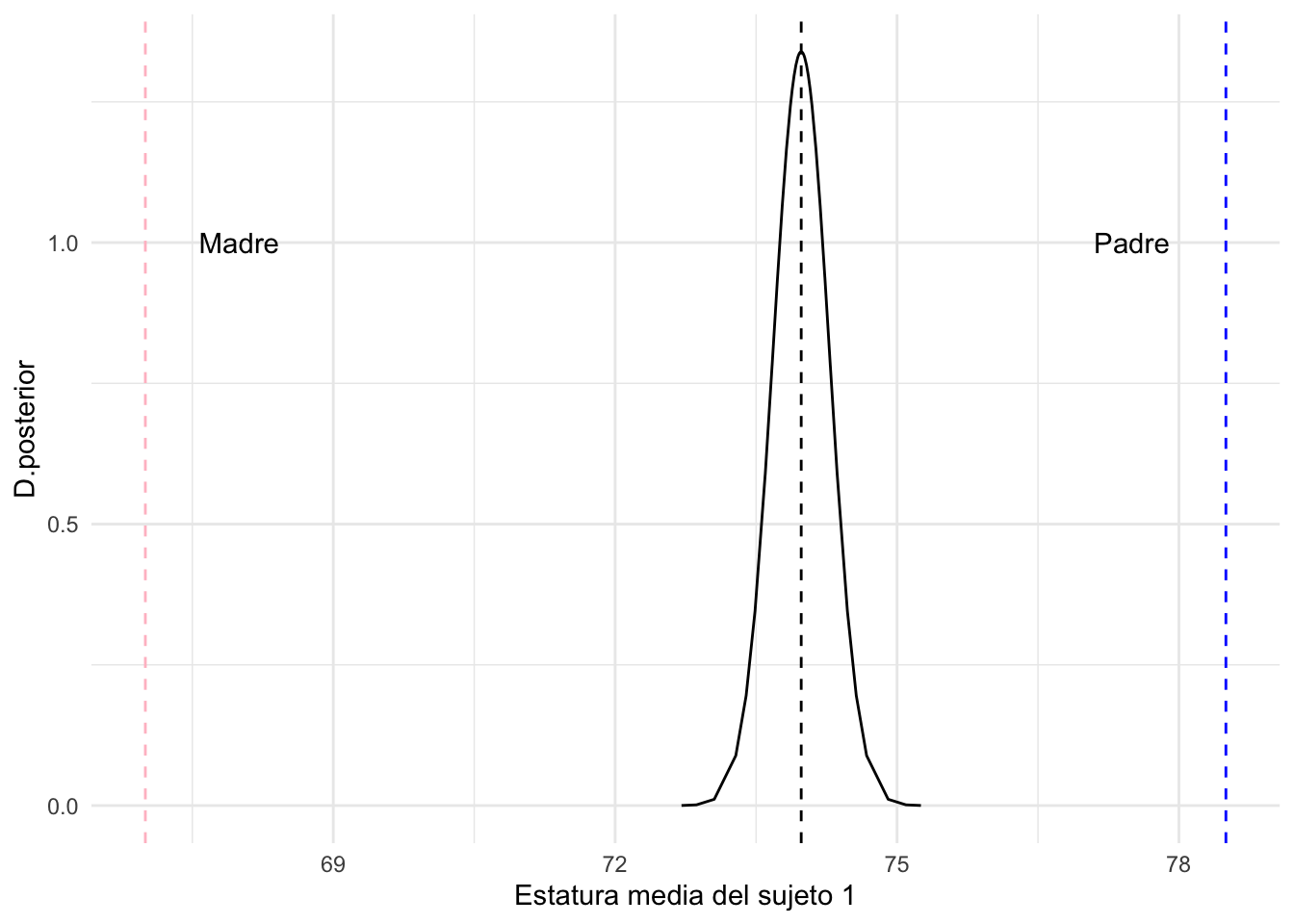

Figura 3.6: Predicción de la estatura del primer sujeto en la muestra

Podemos ir más allá, infiriendo sobre la estatura (esperada) de un sujeto, sea hombre o mujer, cuando su padre mide 1.75m (68.9 pulgadas) y su madre 1.70m (66.9 pulgadas). Expresamos los resultados en centímetros.

new.data=data.frame(Father=c(68.9,68.9),
                    Mother=c(66.9,66.9),
                    Gender=c("M","F"),
                    Height=c(NA,NA))
datos.combinado <- rbind(datos, data.frame(Family=c(NA,NA),new.data,Kids=c(NA,NA)))

## creamos un vector con NA's para observaciones y 1's para predicciones
datos.indicador <- c(rep(NA, nrow(datos)), rep(1, nrow(new.data)))
## reajustamos el modelo añadiendo la opción de predicción de datos
fit.pred <- inla(formula, data = datos.combinado, 
                 control.compute=list(return.marginals.predictor=TRUE),
                 control.predictor = list(link = datos.indicador))
## y describimos los valores ajustados para los escenarios añadidos
round(fit.pred$summary.fitted.values[(nrow(datos)+1):nrow(datos.combinado),]*2.54,1)
#>                       mean  sd 0.025quant 0.5quant
#> fitted.Predictor.899 177.9 0.3      177.3    177.9
#> fitted.Predictor.900 164.7 0.3      164.0    164.7
#>                      0.975quant mode
#> fitted.Predictor.899      178.6   NA
#> fitted.Predictor.900      165.3   NA

También graficar las distribuciones posteriores y calcular las probabilidades, por ejemplo, de que dicho sujeto supere el 1.65m si es mujer, o el 1.78m si es hombre (Figura 3.7).

# Distribuciones predictivas
pred.M=as.data.frame(fit.pred$marginals.fitted.values[[(nrow(datos)+1)]])*2.54
pred.F=as.data.frame(fit.pred$marginals.fitted.values[[(nrow(datos)+2)]])*2.54
d.pred=rbind(pred.M,pred.F)

# atributo Gender
d.pred$Gender=rep(c("M","F"),c(nrow(pred.M),nrow(pred.F)))
# objetivo de estatura
d.pred$obj=rep(c(178,165),c(nrow(pred.M),nrow(pred.F)))

# cálculo de probabilidades
p165F=round(1-inla.pmarginal(165,pred.F),2)
cat(paste("Pr(estatura>165|mujer,padre=175,madre=170)=",p165F))
#> Pr(estatura>165|mujer,padre=175,madre=170)= 0.16
cat("\n")
p178M=round(1-inla.pmarginal(178,pred.M),2)
cat(paste("Pr(estatura>178|hombre,padre=175,madre=170)=",p178M))
#> Pr(estatura>178|hombre,padre=175,madre=170)= 0.42

d.pred$prob=rep(c(p178M,p165F),c(nrow(pred.M),nrow(pred.F)))


ggplot(d.pred,aes(x=x,y=y))+
  geom_line(aes(color=Gender))+
  geom_vline(aes(xintercept=obj),linetype="dashed")+
  facet_wrap(vars(Gender),scales="free")+
  labs(x="Estatura",y="D.posterior")+
    theme(legend.position = "none")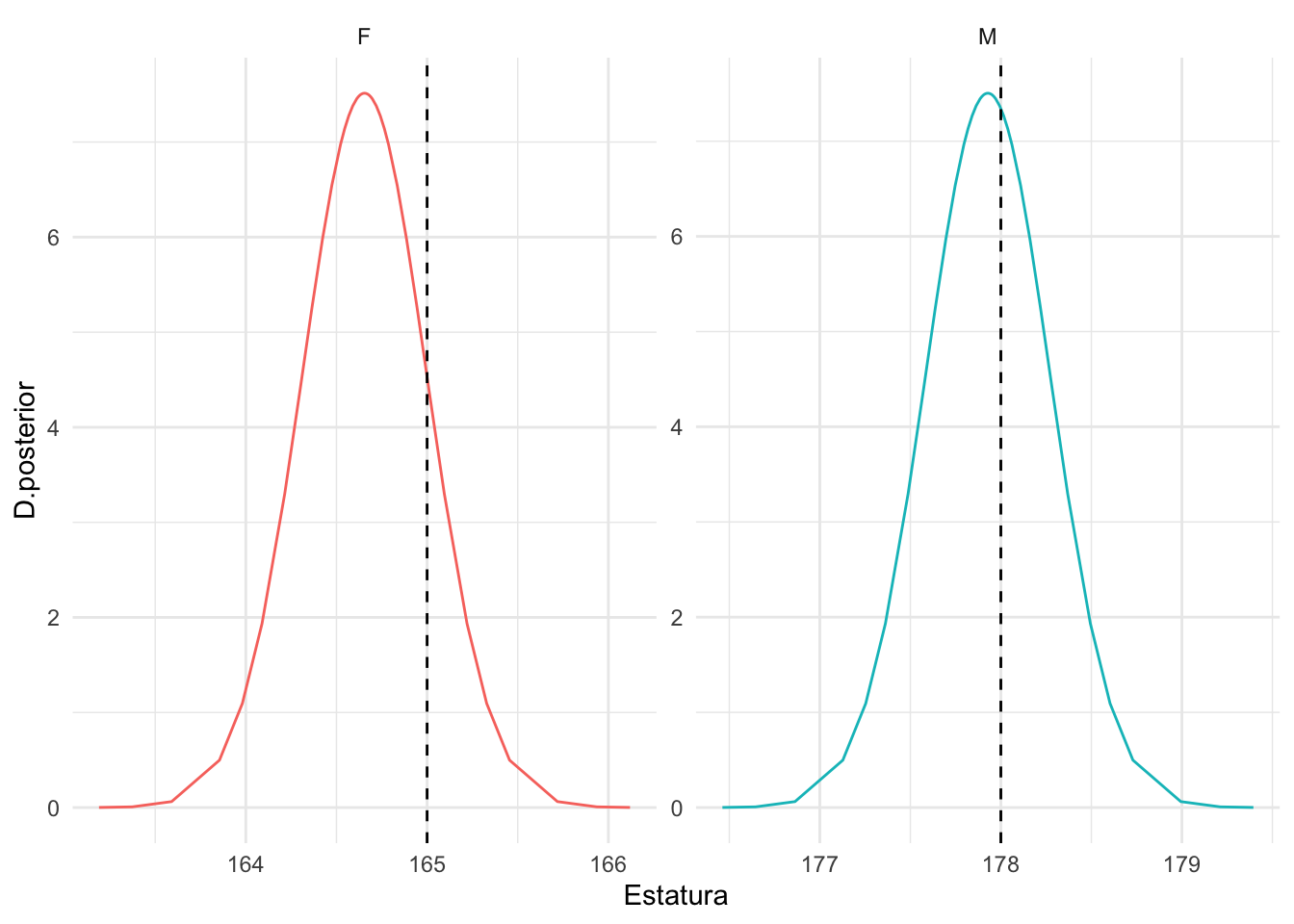

Figura 3.7: Distribución posterior de la estatura de un sujeto cuyo padre mide 1,75cm y madre 1,07cm.

Podríamos también, modificar las especificaciones a priori sobre los parámetros \(\beta_0\) y \(\beta_1\) mediante el comando control.fixed. Por ejemplo, queremos asumir a priori \(\beta_0\sim N(0,10^4)\) y \(\beta_1\sim N(0,100)\) y ver cómo afecta a las inferencias.

fit<-inla(formula,family="gaussian",data=datos,
                   control.fixed=list(mean=0,prec=0.01,
                   mean.intercept=0, prec.intercept=0.0001))
round(fit$summary.fixed,3)
#>               mean    sd 0.025quant 0.5quant 0.975quant
#> (Intercept) 15.335 2.746      9.949   15.335     20.721
#> Father       0.406 0.029      0.349    0.406      0.463
#> Mother       0.322 0.031      0.260    0.322      0.383
#> GenderM      5.225 0.144      4.942    5.225      5.507
#>             mode kld
#> (Intercept)   NA   0
#> Father        NA   0
#> Mother        NA   0
#> GenderM       NA   0

Si queremos especificar medias a priori diferentes para los coeficientes de los distintos regresores, hemos de especificarlos con listas.

fit = inla(formula,family = "gaussian",data=datos,
                   control.fixed=list(mean=list(Father=0.2,Mother=0.1)))
round(fit$summary.fixed,3)
#>               mean    sd 0.025quant 0.5quant 0.975quant
#> (Intercept) 15.345 2.747      9.957   15.345     20.733
#> Father       0.406 0.029      0.349    0.406      0.463
#> Mother       0.321 0.031      0.260    0.321      0.383
#> GenderM      5.226 0.144      4.943    5.226      5.508
#>             mode kld
#> (Intercept)   NA   0
#> Father        NA   0
#> Mother        NA   0
#> GenderM       NA   0

Si queremos modificar la especificación de la prior en \(\sigma^2\), o lo que es equivalente, en la precisión \(\tau\), con la distribución \(log(\tau) \sim N(0,1)\) en lugar de \(\tau \sim Ga(1,10^{-5})\), vemos cómo afecta a la inferencia posterior sobre la precisión.

fit_n = inla(formula,family="gaussian", data=datos,
                   control.family=list(hyper=list(
                     prec=list(prior="gaussian",param=c(0,1)))))
# con el modelo log-gamma para precisión
round(fit$summary.hyperpar,3)
#>                                          mean   sd
#> Precision for the Gaussian observations 0.216 0.01
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations      0.197    0.216
#>                                         0.975quant mode
#> Precision for the Gaussian observations      0.236   NA
# con el modelo normal para precisión
round(fit_n$summary.hyperpar,3)
#>                                          mean   sd
#> Precision for the Gaussian observations 0.216 0.01
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations      0.197    0.216
#>                                         0.975quant mode
#> Precision for the Gaussian observations      0.237   NA

Cuando tenemos información previa disponible sobre la variación de los datos, será generalmente más intuitivo expresarla en términos de la desviación estándar \(\sigma\). Bastará con conseguir la equivalencia en la escala de \(log(\tau)\) para incluirla en el modelo. Por ejemplo, si sabemos que la desviación típica está entre 2 y 14, \(\sigma \sim Unif(2,14)\), podemos calcular una prior para la log-precisión del siguiente modo:

1. simular una muestra de \(\sigma \sim Unif(2,14)\)
2. transformar a precisiones
3. calcular los parámetros de la Gamma para la precisión, a partir de su media y varianza

Hacemos los cálculos y graficamos la prior en la Figura 3.8.

# parámetros para sigma~Un(a1,b1)
a1<-2
b1<-14
# simulamos sigma de una distribución Unif(a1,b1)
sigma<-runif(n=10000,min=a1,max=b1)
# obtenemos la precisión
tau<-1/sigma^2
# Calculamos los parámetros alpha,beta de una distrib. Gamma para la precisión
# mean=alpha/beta; var=alpha/beta^2
beta= mean(tau)/var(tau)
alpha<-mean(tau)*beta
# dibujamos los valores de la precisión
tau.seq=sort(tau)
  # seq(min(tau),max(tau),length=1000)
prior=data.frame(tau=tau.seq,dprior=dgamma(tau.seq,alpha,beta))
ggplot(prior, aes(x=tau))+
  geom_histogram(aes(y=..density..),color="grey",fill="white")+
  geom_line(aes(y=dprior))
#> `stat_bin()` using `bins = 30`. Pick better value with
#> `binwidth`.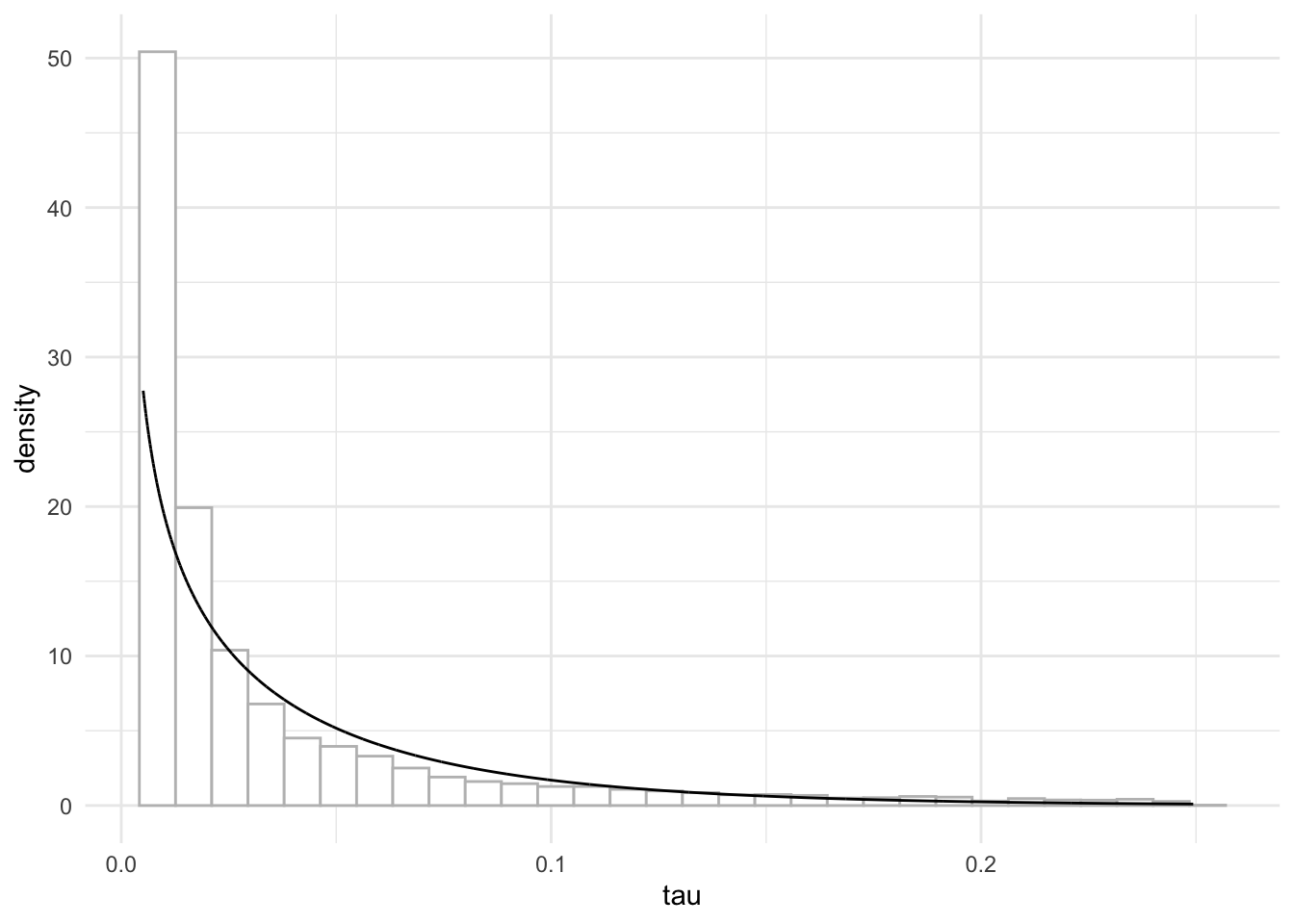

Figura 3.8: Distribución a prior para tau con sigma ~ Uniforme(2,14)

Utilicemos pues esos parámetros para especificar la prior sobre \(\tau\) en INLA:

fit = inla(formula,family="gaussian",data=datos,
                   control.family=list(hyper=list(
                     prec=list(prior="loggamma",param=c(alpha,beta)))))
round(fit$summary.hyperpar,3)
#>                                          mean   sd
#> Precision for the Gaussian observations 0.214 0.01
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations      0.195    0.214
#>                                         0.975quant mode
#> Precision for the Gaussian observations      0.234   NA

3.6 Efectos aleatorios

Desde una perspectiva frecuentista un modelo básico de Anova podría ser un modelo de efectos fijos, pero también de efectos aleatorios. Así por ejemplo el ‘tratamiento’ dado en un ensayo clínico es un efecto relevante para comparar y diferenciar cómo afecta a la respuesta; ‘tratamiento’ sería entonces un efecto fijo, por ser un efecto de interés primario. En otro ejemplo, se han aplicado varios fertilizantes a cultivos en fincas distintas; el interés primario será comparar los fertilizantes, pero la diversidad de fincas solo se ha incluido para introducir variabilidad e incrementar, por supuesto, el número de datos en el estudio; así pues, ‘fertilizante’ será un efecto fijo, pero no es un objetivo comparar las fincas, por lo que se considerará como un efecto aleatorio.

Una variable predictiva, numérica o categórica, entra en el modelo como efecto fijo cuando se piensa que afecta a todas las observaciones del mismo modo, y que su efecto es de interés primario en el estudio. En un contexto bayesiano un efecto fijo tendrá un coeficiente asociado al que se le asigna a menudo una distribución a priori vaga (mínimo informativa), como una gausiana con media cero y varianza (conocida) grande. En cualquier caso, la distribución a priori que se asume para los efectos fijos es siempre una distribución conocida.

Un efecto aleatorio identifica a variables de tipo categórico que no son de interés primario en la investigación, pero que se considera que añaden incertidumbre y por lo tanto variabilidad a la respuesta. La modelización habitual de los efectos aleatorios es una prior gausiana con media cero y una precisión desconocida, para la que será preciso asignar, así mismo, una distribución a priori. La distribución a priori de los efectos aleatorios tiene parámetros desconocidos, llamados hiperparámetros, a los que habrá que asignar también distribuciones a priori.

Puesto que no salimos del modelo lineal, seguiremos asumiendo una respuesta normal, gaussian, con media igual a un predictor lineal \(\mu=\eta=\theta+ Z u\), donde \(Z\) es la correspondiente matriz de diseño para los efectos aleatorios \(z_1, z_2,...\). Se asume además una varianza desconocida \(\sigma^2\).

En INLA la fórmula de predicción de una respuesta \(y\) a partir de un conjunto de efectos aleatorios z1,z2,… se especifica como:

formula = y ~ 1  + f(z1, model="") + f(z2,model="") 

donde la función \(f()\) especifica la relación entre el predictor lineal de la respuesta y los efectos aleatorios \(z\). La función \(f()\) tiene muchos argumentos, que se pueden consultar con el comando ?f. El tipo de relación asumida se incluye en el argumento model o modelo latente, que tiene como posibilidades names(inla.models()$latent). En el modelo lineal, la opción habitual es model="iid", que asume efectos aleatorios independientes e idénticamente distribuidos.

names(inla.models()$latent)
#>  [1] "linear"       "iid"          "mec"         
#>  [4] "meb"          "rgeneric"     "cgeneric"    
#>  [7] "rw1"          "rw2"          "crw2"        
#> [10] "seasonal"     "besag"        "besag2"      
#> [13] "bym"          "bym2"         "besagproper" 
#> [16] "besagproper2" "fgn"          "fgn2"        
#> [19] "ar1"          "ar1c"         "ar"          
#> [22] "ou"           "intslope"     "generic"     
#> [25] "generic0"     "generic1"     "generic2"    
#> [28] "generic3"     "spde"         "spde2"       
#> [31] "spde3"        "iid1d"        "iid2d"       
#> [34] "iid3d"        "iid4d"        "iid5d"       
#> [37] "iidkd"        "2diid"        "z"           
#> [40] "rw2d"         "rw2diid"      "slm"         
#> [43] "matern2d"     "dmatern"      "copy"        
#> [46] "clinear"      "sigm"         "revsigm"     
#> [49] "log1exp"      "logdist"

Veamos cómo ajustar un modelo de efectos aleatorios a partir de un ejemplo sencillo. Comenzamos con la base de datos broccoli en la librería faraway. Varios cultivadores suministran brócoli a una planta de procesamiento de alimentos. La planta da instrucciones a los cultivadores para que empaquen el brócoli en cajas de tamaño estándar. Debe haber 18 racimos de brócoli por caja y cada racimo debe pesar entre 1,33 y 1,5 libras. Debido a que los productores utilizan diferentes variedades, métodos de cultivo, etc., hay cierta variación en el peso de los racimos. El responsable de la planta seleccionó 3 cultivadores al azar y luego 4 cajas al azar suministradas por estos cultivadores. Se seleccionaron 3 racimos de brocoli de cada caja (a modo de repeticiones).

La variable de interés es el peso del racimo de brócoli, en la variable wt. Sin embargo, dado cómo se ha seleccionado la muestra, el objetivo no es ni la comparación entre cultivadores (grower), ni entre cajas (box), asumiendo que tenemos varios racimos (cluster) en cada una de las combinaciones de los anteriores factores. Sin embargo, de manera lógica intuimos que habrá variabilidad entre cajas (efecto aleatorio box) y también entre cultivadores (efecto aleatorio grower), lo que nos conduce a un modelo en el que todos los predictores, box y grower intervienen como efectos aleatorios; la variable cluster la aprovechamos a modo de repeticiones de medidas en una misma caja de un mismo cultivador.

La base de datos cuenta con 36 registros (3 observaciones en cada combinación grower-box.

\[(y_{ijk}|\mu_{ij},\sigma^2 ) \sim N(\mu_{ij},\sigma^2)\]

con \[\eta_{ij} =\mu_{ij}= \theta + \alpha_i^G + \beta_j^B; \ \ i=2,3; j=2,3,4\] el peso medio que comparten todos los racimos en cada combinación de agricultor-caja: \(k=1,2,3\), y donde \(\alpha^G\) representa el efecto aleatorio asociado al cultivador (grower) y \(\beta^B\) a la caja (box).

Así el vector de efectos latentes está compuesto por el efecto fijo de interceptación \(theta\) y los efectos aleatorios \(u=(\alpha_2^G,\alpha_3^G,\beta_2^B,\beta_3^B,\beta_4^B)\).

El siguiente paso es especificar una distribución a priori sobre los parámetros. INLA por defecto asigna una prior difusa sobre la interceptación \(\theta\) y también sobre la precisión de los datos \(\tau=1/\sigma^2\). Dado que los \(\alpha_i^G\) representan el efecto diferencial asociado al cultivador, es razonable asumir independencia entre todos estos parámetros y una distribución idéntica, centrada en el cero (ante ausencia de información) y con una varianza desconocida. Con esto estamos diciendo que en principio no tenemos información sobre que efectivamente el efecto cultivador sea relevante (media cero), pero sí que añade cierta variabilidad \(\sigma_{\alpha}^2\) a la respuesta. Del mismo modo, se asume que los \(\beta_j^B\) son a priori independientes e idénticamente distribuidos (iid) con una normal centrada en el cero (ante ausencia de información) y con varianza desconocida \(\sigma_{\beta}^2\).

\[\begin{eqnarray*} \theta &\sim & N(0,\sigma_{\theta}^2), \ \sigma_{\theta}^2=\infty \\ log(\tau) &\sim & Log-Ga(1,5\cdot 10^{-5})\\ \alpha_i^G & \sim_{iid} & N(0,\sigma_{\alpha}^2), i=2,3 \\ \beta_j^B & \sim_{iid} & N(0,\sigma_{\beta}^2), j=2,3,4 \end{eqnarray*}\]

Surgen pues, dos nuevos parámetros en las a priori, o hiperparámetros, \(\sigma_{\alpha}^2\) y \(\sigma_{\beta}^2\), a los que también habrá que asignar una distribución a priori. Dado que se trata de varianzas, por defecto INLA asume gammas inversas difusas, o lo que es lo mismo, log-gammas difusas para las precisiones

\[\begin{eqnarray*} \tau_{\alpha}=1/\sigma_{\alpha}^2 &\sim & Ga(1,5\cdot 10^{-5}) \\ \tau_{\beta}=1/\sigma_{\beta}^2 &\sim & Ga(1,5\cdot 10^{-5}) \end{eqnarray*}\]

Surgen pues, tres niveles de especificación del modelo: datos, parámetros e hiperparámetros, que generan un modelo jerárquico de tres niveles, y sobre el que hablaremos más adelante.

data(broccoli, package="faraway")
str(broccoli)
#> 'data.frame':    36 obs. of  4 variables:
#>  $ wt     : num  352 369 383 339 367 328 376 359 388 365 ...
#>  $ grower : Factor w/ 3 levels "1","2","3": 1 1 1 2 2 2 3 3 3 1 ...
#>  $ box    : Factor w/ 4 levels "1","2","3","4": 1 1 1 1 1 1 1 1 1 2 ...
#>  $ cluster: Factor w/ 3 levels "1","2","3": 1 2 3 1 2 3 1 2 3 1 ...
formula = wt ~ f(grower,model="iid")+ f(box,model="iid")
fit = inla(formula, family="gaussian",data=broccoli,
           control.compute = list(dic=TRUE,waic=TRUE))  

Cuando queremos mostrar los resultados a posteriori sobre los efectos aleatorios a partir de un ajuste fit con inla, tenemos las siguientes opciones:

• fit$summary.random resume la inferencia posterior sobre los efectos aleatorios
• names(fit$marginals.random) lista los nombre de todos los efectos aleatorios
• fit$marginals.random da las distribuciones posteriores marginales de los efectos aleatorios

fit$summary.random
#> $grower
#>   ID          mean          sd  0.025quant      0.5quant
#> 1  1  4.144038e-07 0.006023482 -0.01225481  3.280315e-07
#> 2  2 -2.900762e-06 0.006023482 -0.01226037 -2.296176e-06
#> 3  3  2.486390e-06 0.006023482 -0.01225133  1.968166e-06
#>   0.975quant mode          kld
#> 1 0.01225620   NA 5.722090e-05
#> 2 0.01225063   NA 5.722103e-05
#> 3 0.01225968   NA 5.722099e-05
#> 
#> $box
#>   ID          mean          sd  0.025quant      0.5quant
#> 1  1  4.758888e-06 0.005802452 -0.01177735  4.049980e-06
#> 2  2 -2.728427e-06 0.005802451 -0.01178779 -2.321988e-06
#> 3  3 -1.205594e-06 0.005802451 -0.01178567 -1.026002e-06
#> 4  4 -8.248796e-07 0.005802451 -0.01178514 -7.020021e-07
#>   0.975quant mode          kld
#> 1 0.01179062   NA 7.668181e-07
#> 2 0.01178018   NA 7.668152e-07
#> 3 0.01178230   NA 7.668141e-07
#> 4 0.01178283   NA 7.668139e-07

Sin embargo, lo relevante en un modelo de efectos aleatorios es la inferencia sobre las varianzas asociadas a los datos, pero también la variabilidad extra que añaden los efectos aleatorios:

fit$summary.hyperpar
#>                                                 mean
#> Precision for the Gaussian observations 3.787215e-03
#> Precision for grower                    3.193648e+04
#> Precision for box                       3.713549e+04
#>                                                   sd
#> Precision for the Gaussian observations 9.074604e-04
#> Precision for grower                    2.255205e+04
#> Precision for box                       2.758028e+04
#>                                           0.025quant
#> Precision for the Gaussian observations 2.297173e-03
#> Precision for grower                    5.890762e+03
#> Precision for box                       9.067258e+03
#>                                             0.5quant
#> Precision for the Gaussian observations 3.689591e-03
#> Precision for grower                    2.627077e+04
#> Precision for box                       2.966319e+04
#>                                           0.975quant mode
#> Precision for the Gaussian observations 5.846180e-03   NA
#> Precision for grower                    9.090582e+04   NA
#> Precision for box                       1.110818e+05   NA

Vemos que tanto la precisión asociada al efecto aleatorio caja (box), como al efecto cultivador, grower, son muy grandes, lo que implica varianzas muy pequeñas que posiblemente nos permitiría prescindir de dichos efectos aleatorios para ajustar un mejor modelo.Cuando transformamos a escala de desviaciones estándar, tenemos la distribución posterior para los tres tipos de error, representados en la Figura 3.9.

nombres=c("sigma","grower","box")
sigma.post=as.data.frame(
  inla.tmarginal(function(tau) tau^(-1/2),
  fit$marginals.hyperpar[[1]]))
sigma.grower.post =as.data.frame(
  inla.tmarginal(function(tau) tau^(-1/2),
  fit$marginals.hyperpar[[2]]))
sigma.box.post = as.data.frame(
  inla.tmarginal(function(tau) tau^(-1/2),
  fit$marginals.hyperpar[[3]]))

sigma=rbind(sigma.post,sigma.grower.post,sigma.box.post)
sigma$efecto=rep(c("sigma","grower","box"),
                 c(nrow(sigma.post),
                   nrow(sigma.grower.post),
                   nrow(sigma.box.post))) 

ggplot(sigma,aes(x=x,y=y)) + 
  geom_line(aes(color=efecto)) +
  labs(x=expression(sigma),y="D.Posterior")+
  facet_wrap(vars(efecto),scales = "free")+
  theme(axis.text.x = element_text(angle = 45),
        legend.position="none")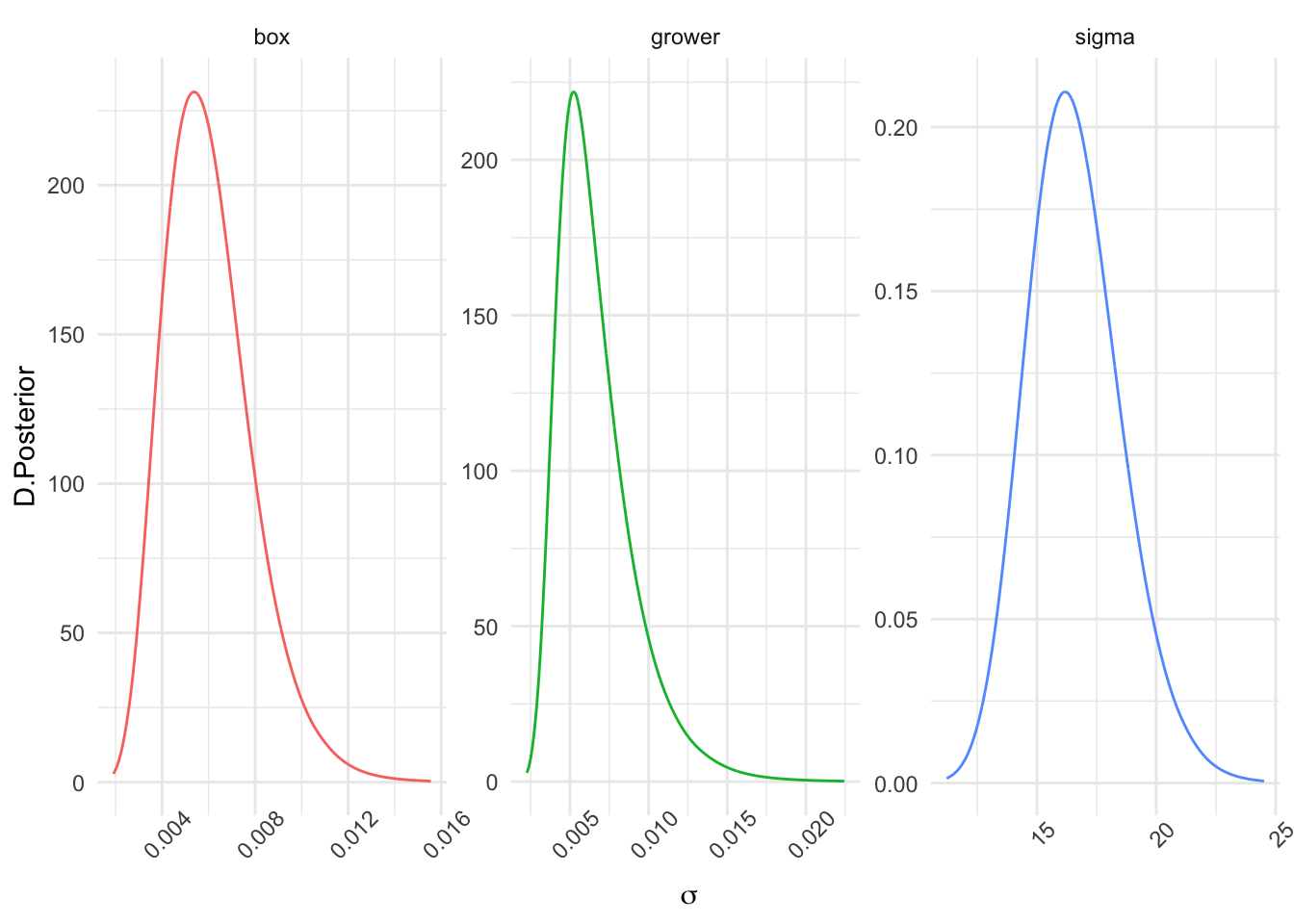

Figura 3.9: Distribución posterior de la desviación típica para las tres fuentes de error: datos, caja y cultivador

No obstante, antes de tomar una decisión sobre la exclusión de los efectos aleatorios, vamos a hacer una aproximación del porcentaje de varianza explicada por cada una de estas fuentes de variación. Utilizando simulaciones de las distribuciones posteriores de \(\sigma^2, \sigma_{\alpha}^2\) y \(\sigma_{\beta}^2\) vamos a calcular la contribución a la varianza del efecto cultivador, \(\sigma_{\alpha}^2/(\sigma^2 + \sigma_{\alpha}^2+\sigma_{\beta}^2)\) y la contribución a la varianza del efecto caja, \(\sigma_{\beta}^2/(\sigma^2 + \sigma_{\alpha}^2+\sigma_{\beta}^2)\). Esto es, vamos a simular de las distribuciones posteriores de las contribuciones a la varianza, y calcular con dichas distribuciones, la probabilidad de que sea suficientemente grande, por ejemplo de que dicha contribución sea mayor a un 1%. Si dicha probabilidad es considerable, estaremos diciendo que el efecto cultivador (o caja) está provocando demasiada variabilidad, indicador de que no se están cumpliendo los estándares de calidad.

\[Pr\left(\frac{\sigma_{\alpha}^2}{\sigma^2 + \sigma_{\alpha}^2+\sigma_{\beta}^2}|y\right) \geq 0.01 ; \ Pr\left(\frac{\sigma_{\beta}^2}{\sigma^2 + \sigma_{\alpha}^2+\sigma_{\beta}^2}|y\right) \geq 0.01\]

n=1000
tau=as.data.frame(
  inla.hyperpar.sample(n,fit,improve.marginals=TRUE))
sigma2=apply(tau,2,function(x) 1/x)
colnames(sigma2)=c("sigma2d","sigma2G","sigma2B")
sigma2=as.data.frame(sigma2)
sigma2=sigma2 %>%
  mutate(contrib.G=sigma2G/(sigma2d+sigma2G+sigma2B),
         contrib.B=sigma2B/(sigma2d+sigma2G+sigma2B))

# contribución a la varianza de grower: Pr(contrib.G>1/100)
cat(paste("Prob.contribución de grower a la varianza > 1%=",
          mean(sigma2$contrib.G > 0.01),"\n"))
#> Prob.contribución de grower a la varianza > 1%= 0
# contribución a la varianza de box: Pr(contrib.B>1/100)
cat(paste("Prob.contribución de box a la varianza > 1%=",
          mean(sigma2$contrib.B > 0.01)))
#> Prob.contribución de box a la varianza > 1%= 0

Ante estos resultados, con probabilidad 0 de que dichos efectos aporten a la varianza más de un 1%, se justifica la opción de prescindir de los efectos grower y box como efectos aleatorios y ajustar el modelo con un único efecto fijo global.

formula = wt ~ 1
fit = inla(formula, family="gaussian",data=broccoli,
           control.compute = list(dic=TRUE,waic=TRUE))  
fit$summary.fixed
#>                 mean       sd 0.025quant 0.5quant
#> (Intercept) 358.1667 2.777017    352.691 358.1667
#>             0.975quant mode         kld
#> (Intercept)   363.6423   NA 1.15452e-08
fit$summary.hyperpar
#>                                                mean
#> Precision for the Gaussian observations 0.003767923
#>                                                   sd
#> Precision for the Gaussian observations 0.0008714431
#>                                          0.025quant
#> Precision for the Gaussian observations 0.002272194
#>                                            0.5quant
#> Precision for the Gaussian observations 0.003687323
#>                                         0.975quant mode
#> Precision for the Gaussian observations 0.00568654   NA

Vemos que la variación en los indicadores DIC (308.0013303) y WAIC (307.8041861) es despreciable para este nuevo modelo.

Inferimos a continuación con las distribuciones posteriores para la media global y la varianza de los datos.

theta.post = as.data.frame(fit$marginals.fixed[[1]])
sigma.post=as.data.frame(inla.tmarginal(function(tau) tau^(-1/2),
  fit$marginals.hyperpar[[1]]))

posterior=rbind(theta.post,sigma.post)
posterior$efecto=rep(c("theta","sigma"),
                     c(nrow(theta.post),nrow(sigma.post)))
ggplot(posterior,aes(x=x,y=y)) + 
  geom_line(aes(color=efecto)) +
  labs(x="",y="D.Posterior")+
  facet_wrap(vars(efecto),scales = "free")+
  theme(legend.position = "none")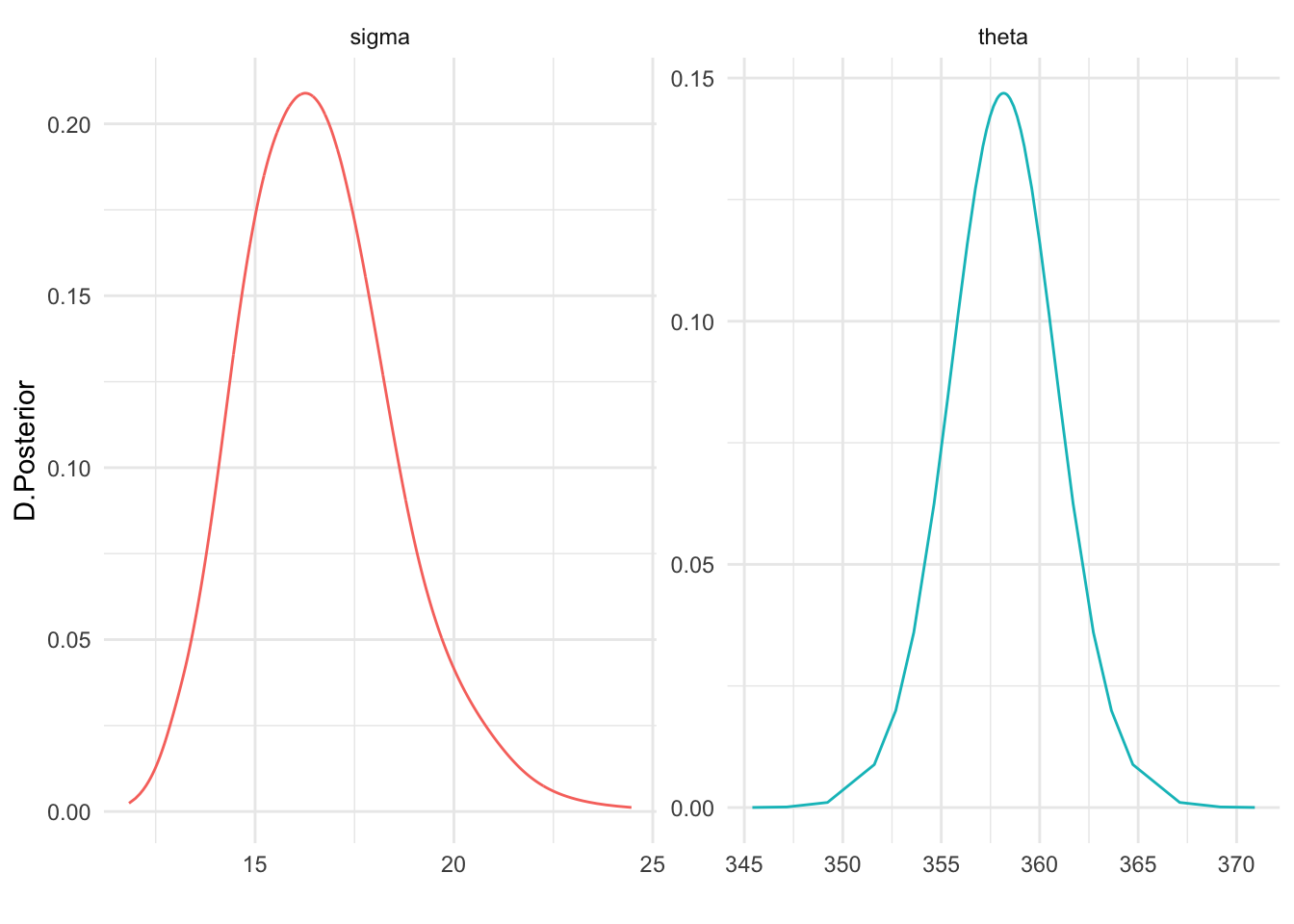

Hemos concluido con este análisis, que todos los cultivadores han respetado los protocolos de calidad establecidos para el empaquetado en cajas.

3.7 Modelos mixtos

En ocasiones cuando ajustamos un modelo lineal tendremos algunos factores de clasificación que operan como efectos fijos y otros que operan como efectos aleatorios. Estaremos ante modelos lineales mixtos. Siendo estrictos, realmente el modelo con solo efectos aleatorios ya es un modelo mixto, puesto que incluye como efecto fijo una interceptación global.

En un modelo lineal mixto seguimos asumiendo una respuesta normal, gaussian, con media igual a un predictor lineal \(\eta=X\beta + Z u\), donde \(X\) es una matriz de diseño con los efectos fijos \(x_1,x_2,...\), y \(Z\) la correspondiente para los efectos aleatorios \(z_1, z_2,...\). Se asume además una varianza desconocida que puede ser distinta para distintos niveles de los predictores, e incluso contener correlaciones entre niveles distintos, y que en general se suele expresar a través de una matriz de covarianzas \(\Sigma\), \((y|\eta,\Sigma) \sim N(\eta,\Sigma)\).

En INLA la fórmula de predicción de una respuesta \(y\) a partir de un conjunto de efectos fijos x1,x2,…, y un conjunto de efectos aleatorios z1,z2,… se especifica como:

formula = y ~ 1 + x1 + x2  + f(z1, model="") + f(z2,model="") 

De nuevo mencionar que la opción más habitual para los efectos aleatorios en un modelo lineal es model="iid".

3.7.1 Datos longitudinales con pendientes iguales

Veamos cómo resolver las inferencias a través de un ejemplo disponible en R-bloggers, proporcionado por Patrick Curran y descargable desde Github. Se refieren estos datos, a un estudio con 405 niños en los dos primeros años de la escuela infantil, medidos a lo largo de cuatro instantes equidistantes (no medidos todos en todos los sujetos) para registrar su progreso en lectura y en comportamiento antisocial. Nos centramos aquí exclusivamente en intentar predecir los progresos en lectura (variable read) para cada sujeto (identificado como id) a lo largo de los 4 instantes de medición (occasion).

Cargamos los datos, prescindimos de los que tienen valores faltantes, y los inspeccionamos en la Figura 3.10.

url="https://raw.githubusercontent.com/BayesModel/data/main/curran_dat.csv"
curran_dat=read.csv(url) %>%
  select(id, occasion, read) %>%
  filter(complete.cases(.))
# el identificador de cada sujeto lo convertimos a factor
curran_dat$id=as.factor(curran_dat$id)
curran_dat$occasion=as.double(curran_dat$occasion)
# Relaciones
g1=ggplot(curran_dat, aes(x=as.factor(occasion),y=read))+
  geom_boxplot()
g2=ggplot(curran_dat, aes(x=occasion,y=read))+
  geom_line(aes(group=id),color="grey",size=0.4)
grid.arrange(g1,g2,ncol=2)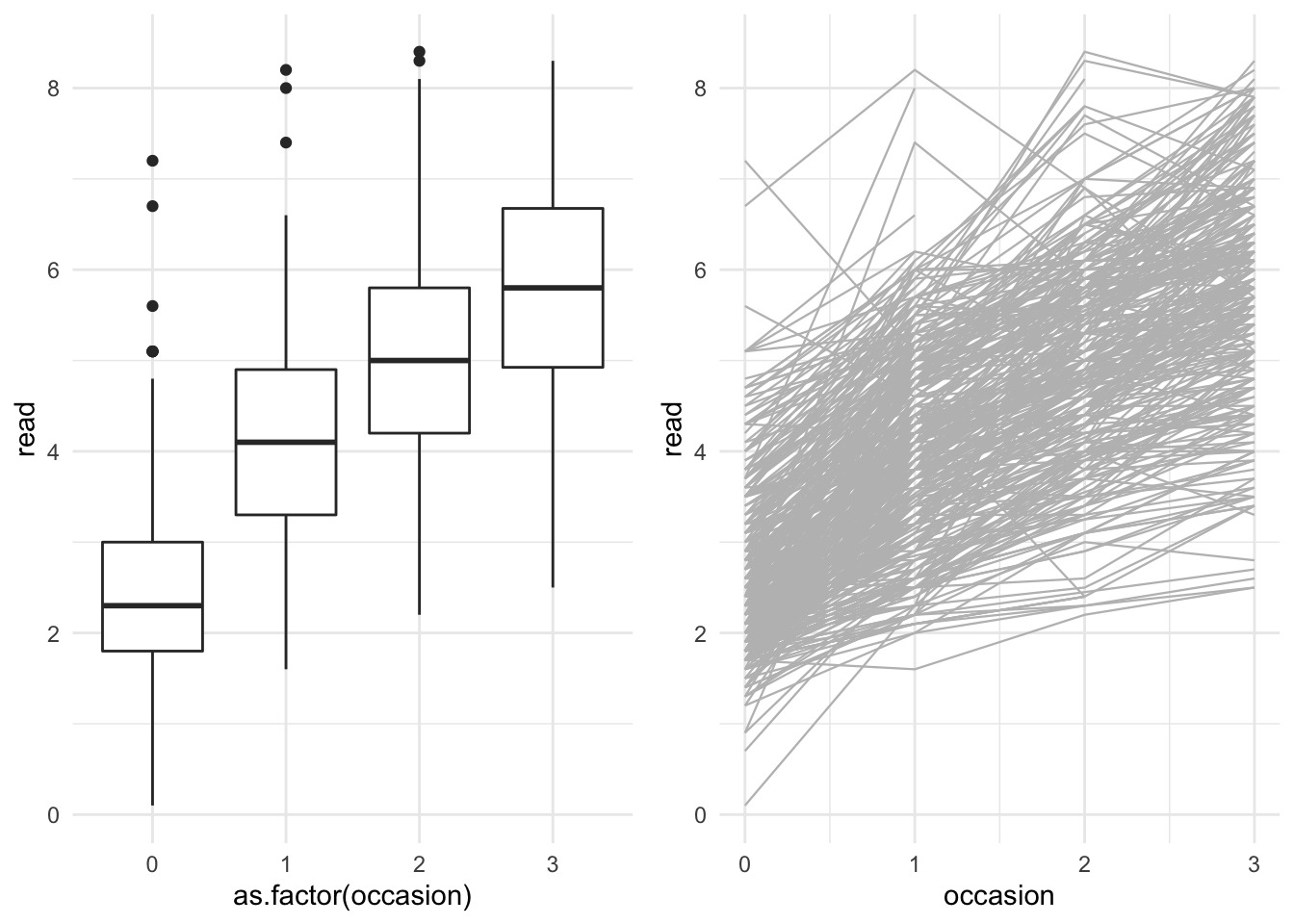

Figura 3.10: Descripción de la BD CurranLong sobre desarrollo de las habilidades lectoras en niños.

Como base vamos a asumir normalidad en la respuesta de un sujeto \(i\) en un instante \(j\), y plantear un modelo lineal para obtener nuestras conclusiones. \[( y_{ij}|\mu_{ij},\sigma^2 ) \sim N(\mu_{ij},\sigma^2); \ i=1,...,450; j=1,2,3,4\]

A la vista de la Figura 3.10 podríamos considerar el tiempo afecta de modo positivo y lineal sobre las habilidades lectoras (a más tiempo, mejores habilidades), lo que convierte a la variable occasion en una covariable numérica (efecto fijo): nos interesará cuantificar cómo afecta el tiempo a la capacidad lectora.

Sin embargo, también en el gráfico apreciamos que cada sujeto arranca de un inicio diferente, o lo que es lo mismo, su recta de predicción tiene una interceptación distinta. Puesto que no nos interesa comparar los individuos, planteamos incorporar un efecto aleatorio del sujeto (variable id). Estamos pues, hablando de predecir la habilidad lectora de un sujeto \(i\) en un instante \(t_{ij}=j\) con:

\[\mu_{ij}=\theta + \alpha_i + \beta \cdot t_{ij} \] con \[\begin{eqnarray*} \text{Nivel II} && \\ \theta &\sim & N(0,100) \\ \beta &\sim& N(0,100) \\ \alpha_i &\sim& N(0,\sigma_{\alpha}^2) \\ \tau=1/\sigma^2 &\sim& Ga(0.001,0.001) \\ \text{Nivel III} && \\ \tau_{\alpha}=1/\sigma_{\alpha}^2 &\sim& Ga(0.001,0.001) \end{eqnarray*}\]

La varianza \(\sigma_{\alpha}^2\) representa la variabilidad existente entre las distintas interceptaciones o niveles cognitivos de los sujetos en el inicio del estudio.

En la Figura 3.11 se muestran las distribuciones posteriores obtenidas sobre efectos fijos y varianzas.

prec.prior=list(prec=list(param=c(0.001,0.001)))
formula= read ~ occasion + f(id,model="iid",hyper = prec.prior) 
fit=inla(formula,family="gaussian",data=curran_dat,
          control.family=list(hyper=prec.prior))
fit$summary.fixed
#>                 mean         sd 0.025quant 0.5quant
#> (Intercept) 2.703751 0.05266758   2.600409 2.703757
#> occasion    1.101333 0.01760829   1.066782 1.101336
#>             0.975quant mode          kld
#> (Intercept)   2.807060   NA 1.200732e-11
#> occasion      1.135862   NA 5.013067e-12
fit$summary.hyperpar
#>                                             mean        sd
#> Precision for the Gaussian observations 2.169736 0.1012852
#> Precision for id                        1.286236 0.1092097
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations   1.975811 2.167867
#> Precision for id                          1.083700 1.281959
#>                                         0.975quant mode
#> Precision for the Gaussian observations   2.374794   NA
#> Precision for id                          1.513686   NA

# Agrupamos todas las distribuciones posteriores
nfixed=length(names(fit$marginals.fixed))
nhyp=length(names(fit$marginals.hyperpar))
res=NULL
for(i in 1:nfixed){
res=rbind(res,data.frame(fit$marginals.fixed[[i]],
                         id=names(fit$marginals.fixed)[i],
                          tipo="fixed"))
}
for(j in 1:nhyp){
    res=rbind(res,data.frame(
    inla.tmarginal(function(tau) tau^(-1/2),fit$marginals.hyperpar[[j]]),
                         id=str_sub(names(fit$marginals.hyperpar)[j], start =15),
                          tipo="sigma"))
}
ggplot(res,aes(x=x,y=y))+
  geom_line(aes(color=id))+
  facet_wrap(vars(tipo),scales="free")+
  theme(legend.position="top",
        legend.title=element_blank(),
        legend.text = element_text(size=5))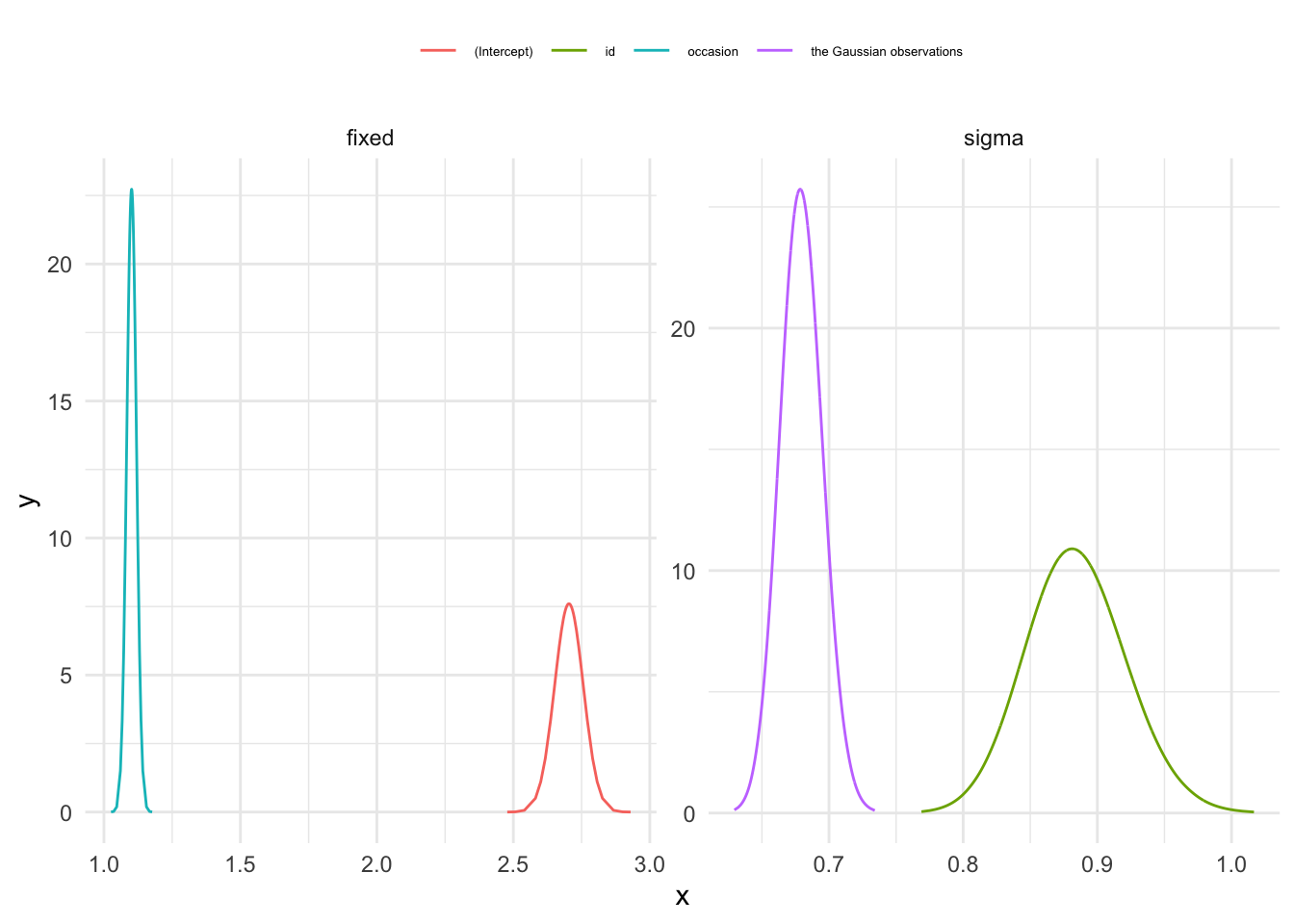

Figura 3.11: Distribuciones posteriores para el modelo con interceptaciones aleatorias por sujeto y efecto fijo del tiempo.

3.7.2 Datos longitudinales con pendientes distintas

Belenky et al. (2003) describen un estudio de los tiempos de reacción en pacientes a los que se ha privado de sueño durante 10 días; cada día se ha ido registrando la respuesta para cada uno de los 18 sujetos en el estudio. Los datos están disponibles como sleepstudy en la librería lme4 y tienen como variables el tiempo medio de reacción en microsegundos (Reaction), el número de días con privación de sueño (Days) y un id para cada sujeto (Subject). Los tiempos de reacción se transforman a segundos para tener mayor estabilidad. Aun así, en la Figura 3.12 se aprecia que el número de días de falta de sueño afecta de modo distinto a cada sujeto.

data(sleepstudy,package="lme4")
sleepstudy$Reaction <- sleepstudy$Reaction / 1000
ggplot(sleepstudy,aes(x=Days,y=Reaction))+
  geom_point(size=0.5)+
  geom_smooth(method="lm",color="blue",size=0.5)+
  facet_wrap(vars(Subject),ncol=6)+
  theme(axis.text.x = element_text(size=5),
        axis.text.y = element_text(size=5))
#> `geom_smooth()` using formula 'y ~ x'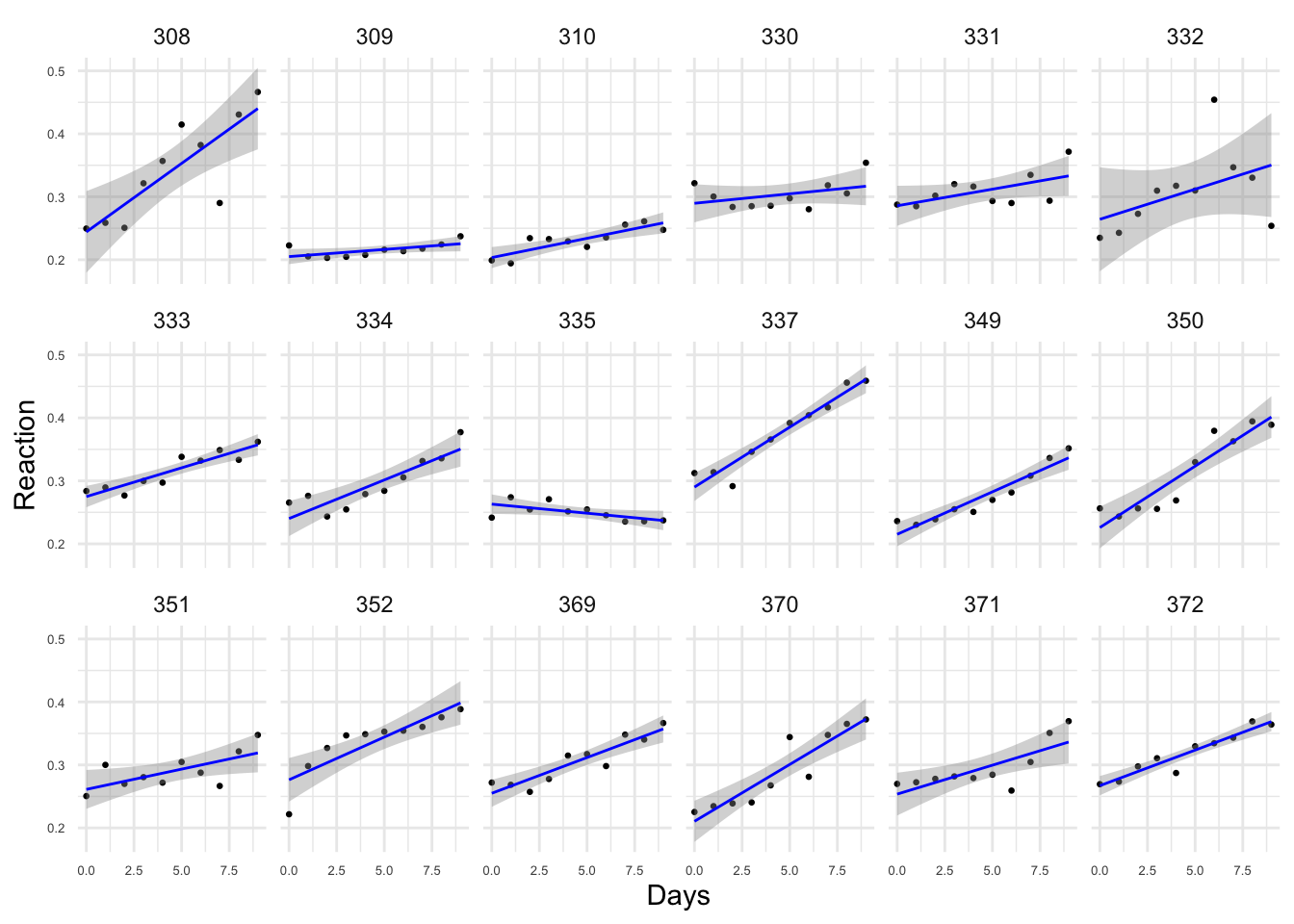

Figura 3.12: Tiempos de reacción en función del número de días con falta de sueño (sleepstudy) para los 18 sujetos en el estudio

Un modelo razonable para estos datos es un modelo lineal que relacione los tiempos de reacción con los días, pero que tenga interceptaciones y pendientes diferentes para cada sujeto. El efecto sujeto entraría en el modelo como un efecto aleatorio para relacionar todos los datos del mismo sujeto sin perder la asunción de independencia entre las observaciones de sujetos distintos. Si llamamos \(y=Reaction\) a la respuesta, estaríamos planteando el siguiente modelo:

\[ y_{ij}|\mu_{ij},\sigma^2 \sim N(\mu,\sigma^2), i=1,...,18; j=1, ...,10\]

con

\[\mu_{ij}=\theta + \alpha_i + \beta \cdot x_{ij} + \gamma_{ij}\]

donde el predictor \(x\) es la variable Days, \((\theta,\beta)\) se tratarían como efectos fijos con a prioris difusas ante falta de información, y \((\alpha_i,\gamma_{ij})\) como efectos aleatorios, con normales centradas en cero y una varianza desconocida a la que habría que asignar así mismo, una distribución a priori. El modelo jerárquico que surge es pues:

\[\begin{eqnarray*} \text{Nivel I} && \\ y_{ij}|\mu_{ij},\sigma^2 &\sim& N(\mu,\sigma^2), i=1,...,18; j=1, ...,10 \\ \text{Nivel II} && \\ \theta &\sim & N(0,1000) \\ \beta &\sim& N(0,1000) \\ \alpha_i &\sim& N(0,\sigma_{\alpha}^2) \\ \gamma_{ij} &\sim & N(0,\sigma_{\gamma})^2 \\ \tau=1/\sigma^2 &\sim& Ga(0.001,0.001)\\ \text{Nivel III} && \\ \tau_{\alpha}=1/\sigma_{\alpha}^2 &\sim& Ga(0.001,0.001) \\ \tau_{\gamma}=1/\sigma_{\alpha}^2 &\sim& Ga(0.001,0.001) \end{eqnarray*}\]

En INLA modelizamos esta propuesta utilizando como predictores;

• la covariable para generar una interceptación ‘media’ (efecto fijo),
• el efecto aleatorio de cada sujeto para generar interceptaciones distintas,
• la interacción entre la covariable y el efecto aleatorio, a través de la matriz de diseño que hemos de construir específicamente, y definir en paralelo un índice de la misma dimensión de los datos, para aplicarla. En la interacción la primera variable define el número de grupos y la segunda el valor de la covariable.

prec.prior=list(prec=list(param=c(0.001,0.001)))
# matriz de diseño para la interacción
Z <- as(model.matrix( ~ 0 + Subject:Days, data = sleepstudy), "Matrix")
# índice para aplicar la matriz de diseño
DayR=1:nrow(sleepstudy)
formula= Reaction ~ Days + f(Subject,model="iid",hyper=prec.prior)+
  f(DayR,model="z",Z=Z,hyper = prec.prior) 
fit=inla(formula,family="gaussian",data=sleepstudy,
         control.compute=list(config=TRUE))
#> Warning in inla.model.properties.generic(inla.trim.family(model), mm[names(mm) == : Model 'z' in section 'latent' is marked as 'experimental'; changes may appear at any time.
#>   Use this model with extra care!!! Further warnings are disabled.
#> as(<dgCMatrix>, "dgTMatrix") is deprecated since Matrix 1.5-0; do as(., "TsparseMatrix") instead

Obtenemos en consecuencia, efectos fijos e hiperparámetros, cuyas inferencias posteriores se resumen con:

round(fit$summary.fixed,3)
#>              mean    sd 0.025quant 0.5quant 0.975quant mode
#> (Intercept) 0.251 0.008      0.236    0.251      0.267   NA
#> Days        0.010 0.003      0.004    0.010      0.017   NA
#>             kld
#> (Intercept)   0
#> Days          0
round(fit$summary.hyperpar,3)
#>                                             mean       sd
#> Precision for the Gaussian observations 1566.713  182.872
#> Precision for Subject                   1314.753  571.889
#> Precision for DayR                      6067.457 2128.985
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations   1231.362 1558.539
#> Precision for Subject                      520.885 1209.118
#> Precision for DayR                        2819.871 5762.944
#>                                         0.975quant mode
#> Precision for the Gaussian observations   1950.856   NA
#> Precision for Subject                     2728.329   NA
#> Precision for DayR                       11105.470   NA

Y los efectos aleatorios:

names(fit$marginals.random)
#> [1] "Subject" "DayR"
head(fit$summary.random$Subject)
#>    ID         mean         sd    0.025quant     0.5quant
#> 1 308 -0.003768865 0.01446453 -0.0322859823 -0.003748481
#> 2 309 -0.037614947 0.01485945 -0.0674456412 -0.037392773
#> 3 310 -0.038204849 0.01487071 -0.0680611455 -0.037981148
#> 4 330  0.028705978 0.01469940  0.0002843552  0.028533721
#> 5 331  0.025993632 0.01465099 -0.0023753048  0.025835644
#> 6 332  0.009899239 0.01447474 -0.0184010224  0.009836397
#>     0.975quant mode          kld
#> 1  0.024632711   NA 5.824740e-09
#> 2 -0.009029223   NA 2.027859e-08
#> 3 -0.009601950   NA 2.046395e-08
#> 4  0.058095493   NA 1.427015e-08
#> 5  0.055251159   NA 1.290462e-08
#> 6  0.038554305   NA 6.836886e-09
head(fit$summary.random$DayR)
#>   ID         mean          sd   0.025quant     0.5quant
#> 1  1 6.924213e-06 0.001501481 -0.002937713 6.924417e-06
#> 2  2 1.056644e-02 0.004274276  0.002188708 1.055373e-02
#> 3  3 2.106572e-02 0.008121903  0.005144073 2.103765e-02
#> 4  4 3.184263e-02 0.012056270  0.008205544 3.180030e-02
#> 5  5 4.249502e-02 0.016013234  0.011099076 4.243830e-02
#> 6  6 5.322668e-02 0.019979618  0.014052978 5.315583e-02
#>   0.975quant mode          kld
#> 1 0.00295156   NA 5.527427e-11
#> 2 0.01901744   NA 7.952157e-09
#> 3 0.03714924   NA 1.020988e-08
#> 4 0.05572395   NA 1.066188e-08
#> 5 0.07421818   NA 1.083089e-08
#> 6 0.09280920   NA 1.090792e-08

En la Figura 3.13 mostramos los datos y también los valores ajustados para las rectas, en términos de las interceptaciones y pendientes medias de las correspondientes distribuciones posteriores, además de la banda de estimación que construimos con los correspondientes percentiles de las posterioris.

sleepstudy.pred = sleepstudy %>%
  mutate(fitted=fit$summary.fitted.values$mean,
         rc.low=fit$summary.fitted.values$"0.025quant",
         rc.up=fit$summary.fitted.values$"0.975quant") 

ggplot(sleepstudy.pred,aes(x=Days,y=Reaction))+
  geom_point(size=0.5)+
  geom_line(aes(y=fitted),color="blue")+
  geom_line(aes(y= rc.low),color="skyblue")+
  geom_line(aes(y=rc.up),color="skyblue")+
  facet_wrap(vars(Subject),ncol=6)+
  theme(axis.text.x = element_text(size=5),
        axis.text.y = element_text(size=5))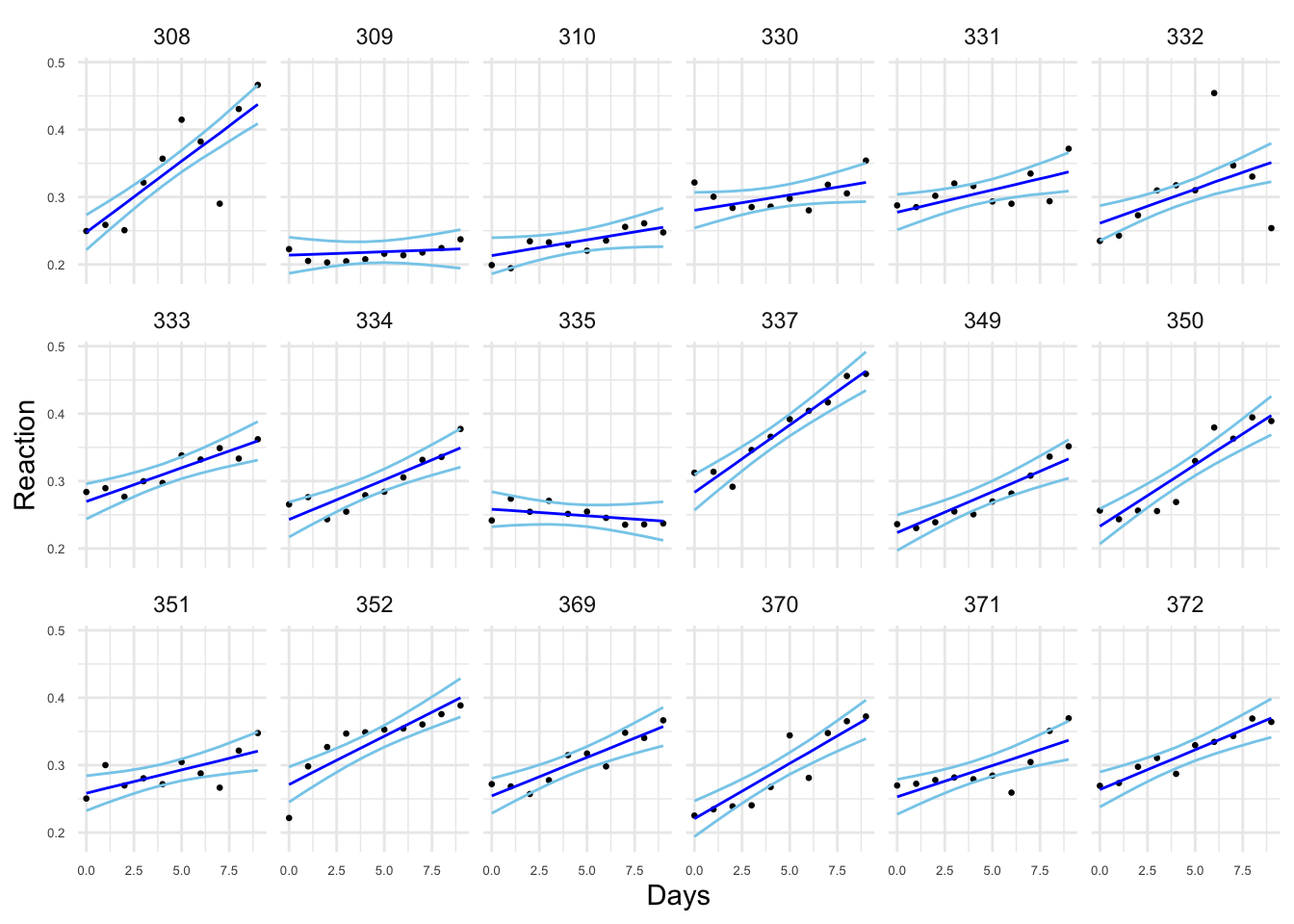

Figura 3.13: Estimaciones posteriores de los predictores lineales: medias y RC.

En la Figura 3.14 mostramos la distribución posterior de los errores de datos y aleatorios.

nhyp=length(names(fit$marginals.hyperpar))
res=NULL
for(j in 1:nhyp){
    res=rbind(res,data.frame(
    inla.tmarginal(function(tau) tau^(-1/2),fit$marginals.hyperpar[[j]]),
                         id=str_sub(names(fit$marginals.hyperpar)[j], start =15)))
}
ggplot(res,aes(x=x,y=y))+
  geom_line(aes(color=id))+
  labs(x=expression(sigma),y="")+
  theme(legend.position="top",
        legend.title=element_blank(),
        legend.text = element_text(size=5))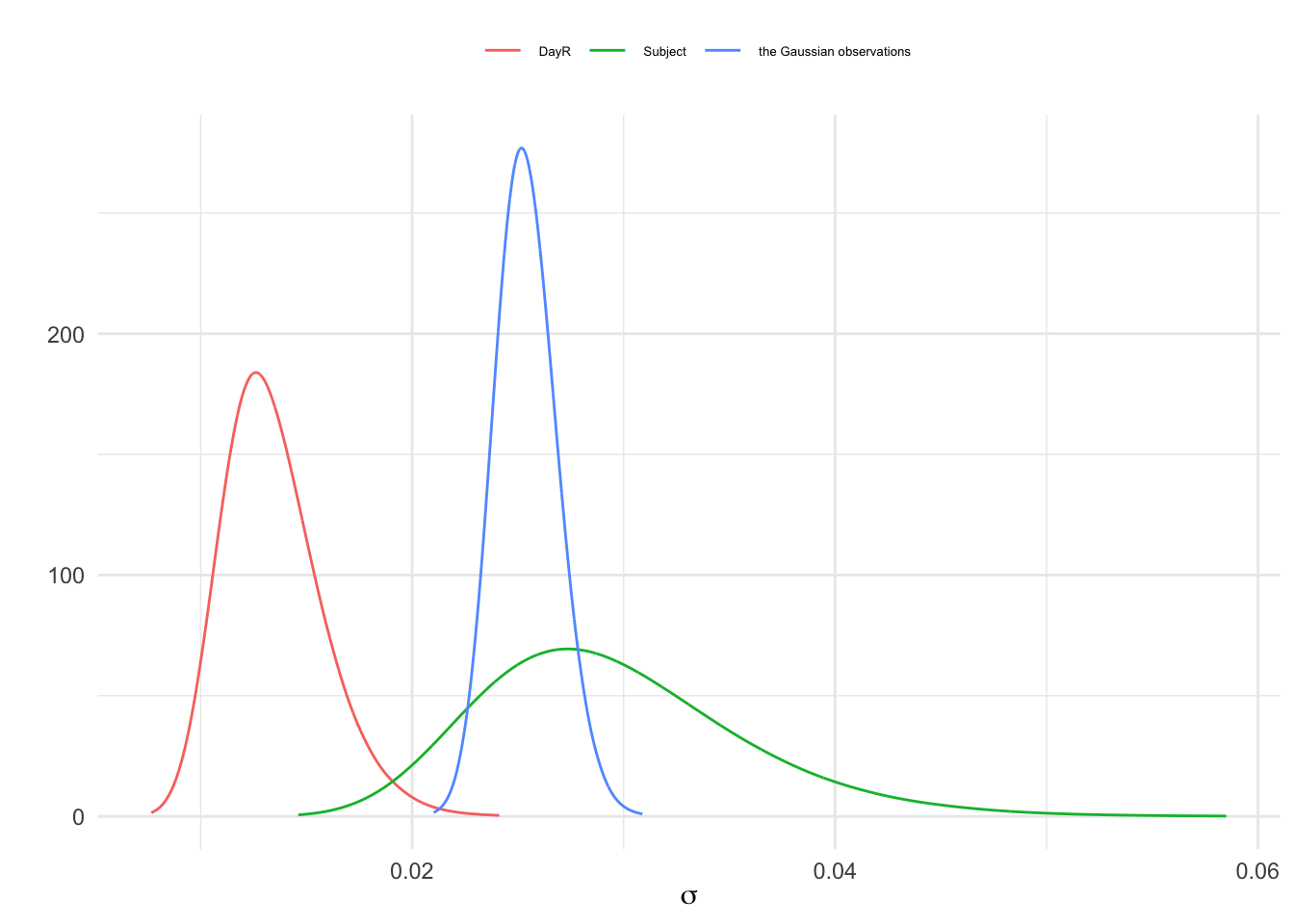

Figura 3.14: Distribución posterior del error de los datos y el error aleatorio

3.7.3 Efectos anidados

Hablamos de efectos anidados cuando cada miembro de un grupo está contenido completamente dentro de una única unidad de otro grupo. Que un factor A esté anidado en otro B, implica que cada nivel de B contiene niveles distintos de A, esto es, cada nivel de A está vinculado solo a algún nivel de B.

La base de datos eggs en la librería faraway nos resulta útil para describir este tipo de modelos con efectos anidados. Estos datos son los resultantes de un experimento para testar la consistencia en los tests de laboratorio que realizaban laboratorios distintos, técnicos distintos. Para ello se dividió en varias muestras un tarro de polvo de huevo seco homogeneizado (con idéntico contenido graso). Se enviaron 4 muestras a cada uno de los 6 laboratorios. De esas 4 muestras, 2 se etiquetaron como G y 2 como H (aun siendo idénticas). Se dieron instrucciones a los laboratorios de dar dos muestras a dos técnicos distintos. Los técnicos recibieron instrucciones de dividir sus muestras en dos partes y medir el contenido graso de cada una. Así, cada laboratorio reportó 8 mediciones del contenido graso (Fat), cada técnico 4 mediciones, con 2 réplicas en cada una de las dos muestras.

Realmente, el laboratorio, el técnico y la muestra solo deberían generar variabilidad en la respuesta, pero en ningún caso generar mediciones distintas. Estamos pues interesados en investigar la magnitud del error debido al laboratorio, al técnico y a la identificación de muestras. Es por ello que tiene sentido considerarlos efectos aleatorios.

Tenemos así en este ejemplo, a los técnicos (Technician) anidados en los laboratorios (Lab). En la Figura 3.15 se muestra claramente la variación entre laboratorios, entre técnicos, y debida al efecto irreal de tener dos muestras distintas G y H (Sample).

data(eggs,package="faraway")
ggplot(eggs,aes(x=Lab,y=Fat))+
  geom_boxplot(aes(color=Technician))+
  facet_wrap(vars(Sample))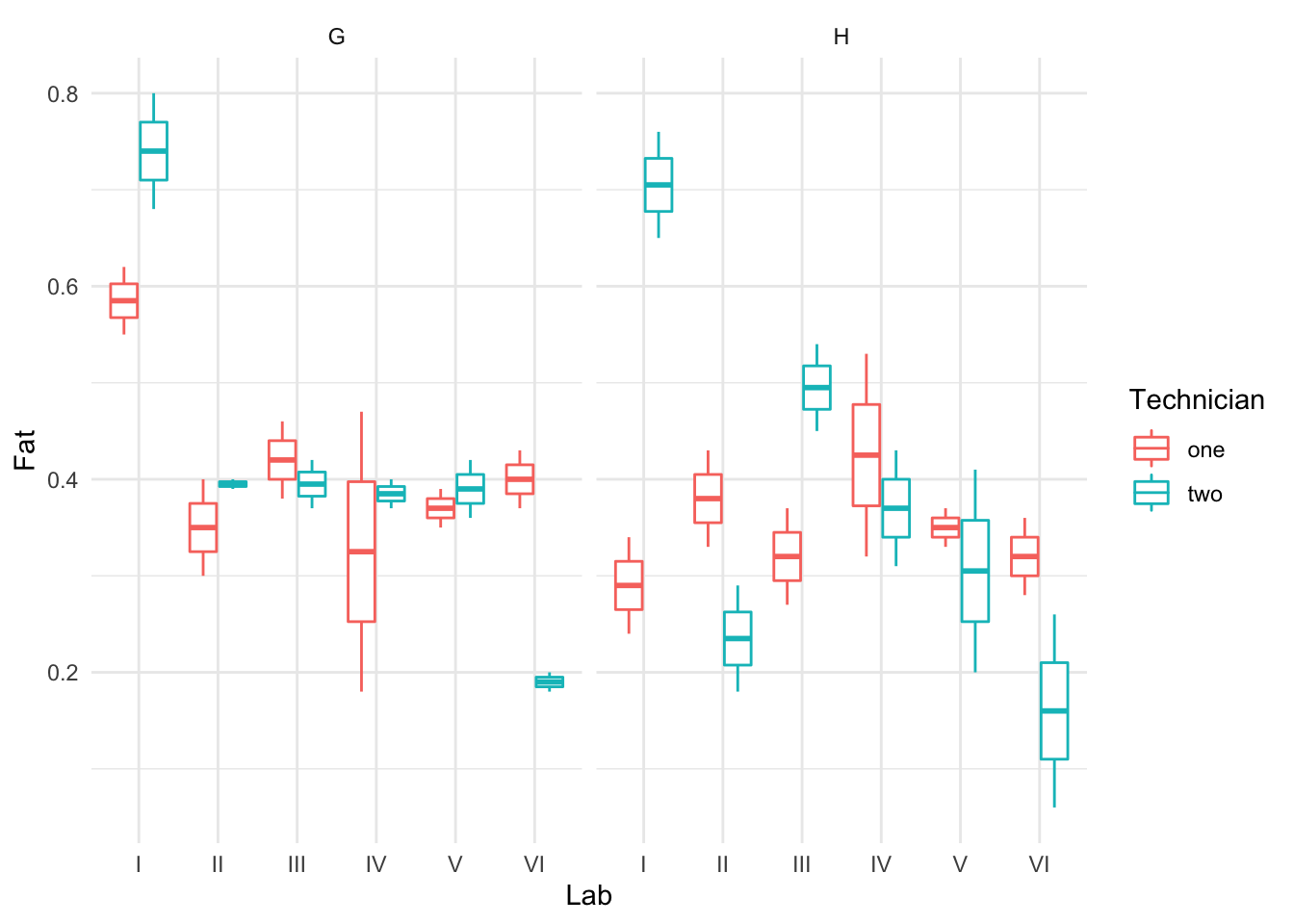

Figura 3.15: Descripción de eggs: variación entre laboratorios y técnicos.

El modelo que planteamos para estimar la respuesta \(y_{ijk}\), contenido graso de la muestra \(k\) (\(k=1,2\)) del laboratorio \(i\) (\(i=1,...,6\)), por el técnico \(j\) (\(j=1,2\)) está basado como siempre, en el modelo normal, \((y_{ijk}|\mu_{ijk},\sigma^2) \sim N(\mu_{ijk},\sigma^2)\), con una media o predictor lineal representado por:

\[ \mu_{ijk}= \theta + \alpha_i^{lab} + \beta_{j:i}^{tec} + \gamma_{k:(j:i)}^{sam}\] y asumiendo en un segundo nivel del modelo las distribuciones a priori: \[\begin{eqnarray*} \theta &\sim& N(0,1000) \\ \tau=1/\sigma^2 &\sim& Ga(0.001,0.001) \\ \alpha_i^{lab}&\sim& N(0,\sigma_{lab}^2); \ i = 1,...,4 \\ \beta_{j:i}^{tec}&\sim& N(0,\sigma_{tec}^2); \ j:i = 1,...,12 \\ \gamma_{k:(j:i)}^{sam}&\sim& N(0,\sigma_{sam}^2); \ k:(j:i)=1,...,24 \end{eqnarray*}\]

El tercer nivel recibiría las distribuciones a priori para los hiperparámetros \(\sigma_{lab}^2, \sigma_{tec}^2,\sigma_{sam}^2\), sobre los que interesa inferir. A priori, con mínima información asumiremos \(GaI(0.001,0.001)\).

Para especificar en INLA los efectos anidados hemos de recurrir a la matriz del modelo, model.matrix(), para crear las matrices de los efectos aleatorios anidados.

A continuación hemos de crear los correspondientes índices, de longitud similar a la del número de registros en la base de datos, para aplicarles las correspondientes matrices de efectos anidados, y ya proceder con el ajuste como habitualmente hacemos.

# matrices de efectos aleatorios anidados
Zlt <- as(model.matrix( ~ 0 + Lab:Technician, data = eggs), "Matrix")
Zlts <- as(model.matrix( ~ 0 + Lab:Technician:Sample, data = eggs), "Matrix")

# índices para aplicar los efectos aleatorios
eggs$IDt = eggs$IDts = 1:nrow(eggs)

# Ajuste
prec.prior=list(prec=list(param=c(0.001,0.001)))
formula = Fat ~ 1 + f(Lab,model="iid",hyper=prec.prior) +
  f(IDt,model="z",Z=Zlt,hyper=prec.prior)+
  f(IDts,model="z",Z=Zlts,hyper=prec.prior)

fit <- inla(formula,data = eggs, 
            control.predictor = list(compute = TRUE), 
            control.family=list(hyper=prec.prior),
            control.fixed=list(prec.intercept=0.001))
# inferencias de interés
round(fit$summary.hyperpar,4)
#>                                             mean       sd
#> Precision for the Gaussian observations 142.0225  39.6761
#> Precision for Lab                       349.8934 651.1007
#> Precision for IDt                       206.0385 210.4850
#> Precision for IDts                      366.9361 335.2768
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations    77.8358 137.4888
#> Precision for Lab                          22.4898 170.1990
#> Precision for IDt                          26.6551 144.1411
#> Precision for IDts                         59.8945 270.7231
#>                                         0.975quant mode
#> Precision for the Gaussian observations   232.9084   NA
#> Precision for Lab                        1808.5266   NA
#> Precision for IDt                         762.1773   NA
#> Precision for IDts                       1256.5371   NA

nhyp=length(names(fit$marginals.hyperpar))
res=NULL
for(j in 1:nhyp){
    res=rbind(res,data.frame(
    inla.tmarginal(function(tau) tau^(-1/2),fit$marginals.hyperpar[[j]]),
                         id=str_sub(names(fit$marginals.hyperpar)[j], start =15)))
}
ggplot(res,aes(x=x,y=y))+
  geom_line(aes(color=id))+
  labs(x=expression(sigma),y="")+
  theme(legend.position="top",
        legend.title=element_blank(),
        legend.text = element_text(size=5))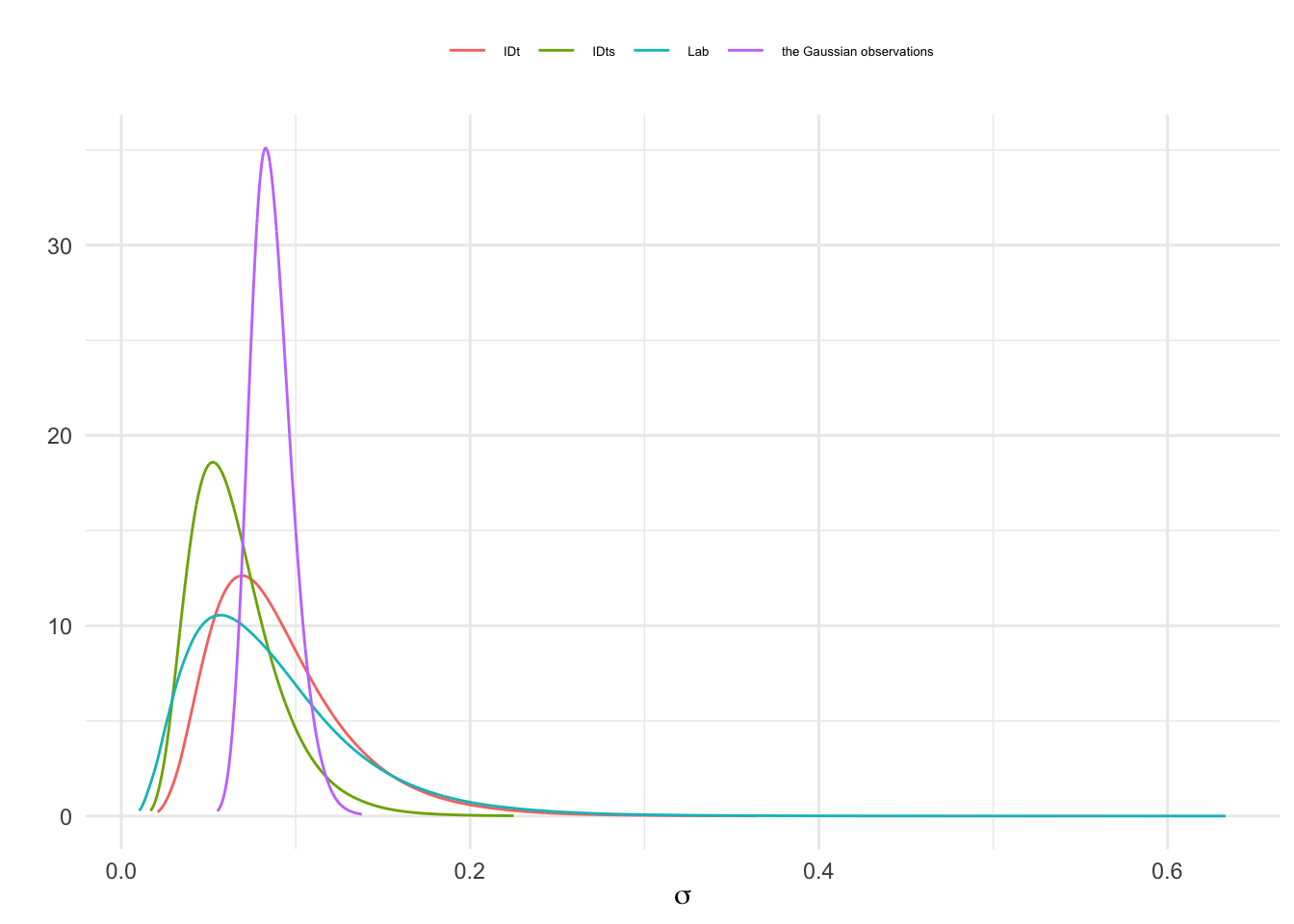

Figura 3.16: Distribución posterior del error de los datos y el error aleatorio

Alternativamente podríamos crear una variable índice a partir de las matrices de efectos aleatorios, para utilizarlas con model="iid" para describir los efectos aleatorios:

eggs$labtech <- as.factor(apply(Zlt, 1, function(x){names(x)[x == 1]}))
eggs$labtechsamp <- as.factor(apply(Zlts, 1, function(x){names(x)[x == 1]}))

formula=Fat ~ 1 + f(Lab, model = "iid", hyper = prec.prior) +
    f(labtech, model = "iid", hyper = prec.prior) +
  f(labtechsamp, model = "iid", hyper = prec.prior)
fit=inla(formula, data = eggs, 
            control.predictor = list(compute = TRUE), 
            control.family=list(hyper=prec.prior),
         control.fixed=list(prec.intercept=0.001))
round(fit$summary.fixed,4)
#>               mean     sd 0.025quant 0.5quant 0.975quant
#> (Intercept) 0.3875 0.0554     0.2756   0.3875     0.4994
#>             mode kld
#> (Intercept)   NA   0
round(fit$summary.hyperpar,4)
#>                                             mean       sd
#> Precision for the Gaussian observations 141.9197  39.6190
#> Precision for Lab                       349.8789 651.1368
#> Precision for labtech                   206.0022 210.4348
#> Precision for labtechsamp               366.9490 335.2905
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations    77.8104 137.3975
#> Precision for Lab                          22.4864 170.1808
#> Precision for labtech                      26.6562 144.1204
#> Precision for labtechsamp                  59.8966 270.7319
#>                                         0.975quant mode
#> Precision for the Gaussian observations   232.6614   NA
#> Precision for Lab                        1808.5293   NA
#> Precision for labtech                     762.0085   NA
#> Precision for labtechsamp                1256.5854   NA

En la Figura 3.17 se muestra la distribución posterior del error de los datos y de los errores aleatorios.

nhyp=length(names(fit$marginals.hyperpar))
res=NULL
for(j in 1:nhyp){
    res=rbind(res,data.frame(
    inla.tmarginal(function(tau) tau^(-1/2),fit$marginals.hyperpar[[j]]),
                         id=str_sub(names(fit$marginals.hyperpar)[j], start =15)))
}
ggplot(res,aes(x=x,y=y))+
  geom_line(aes(color=id))+
  labs(x=expression(sigma),y="")+
  theme(legend.position="top",
        legend.title=element_blank(),
        legend.text = element_text(size=5))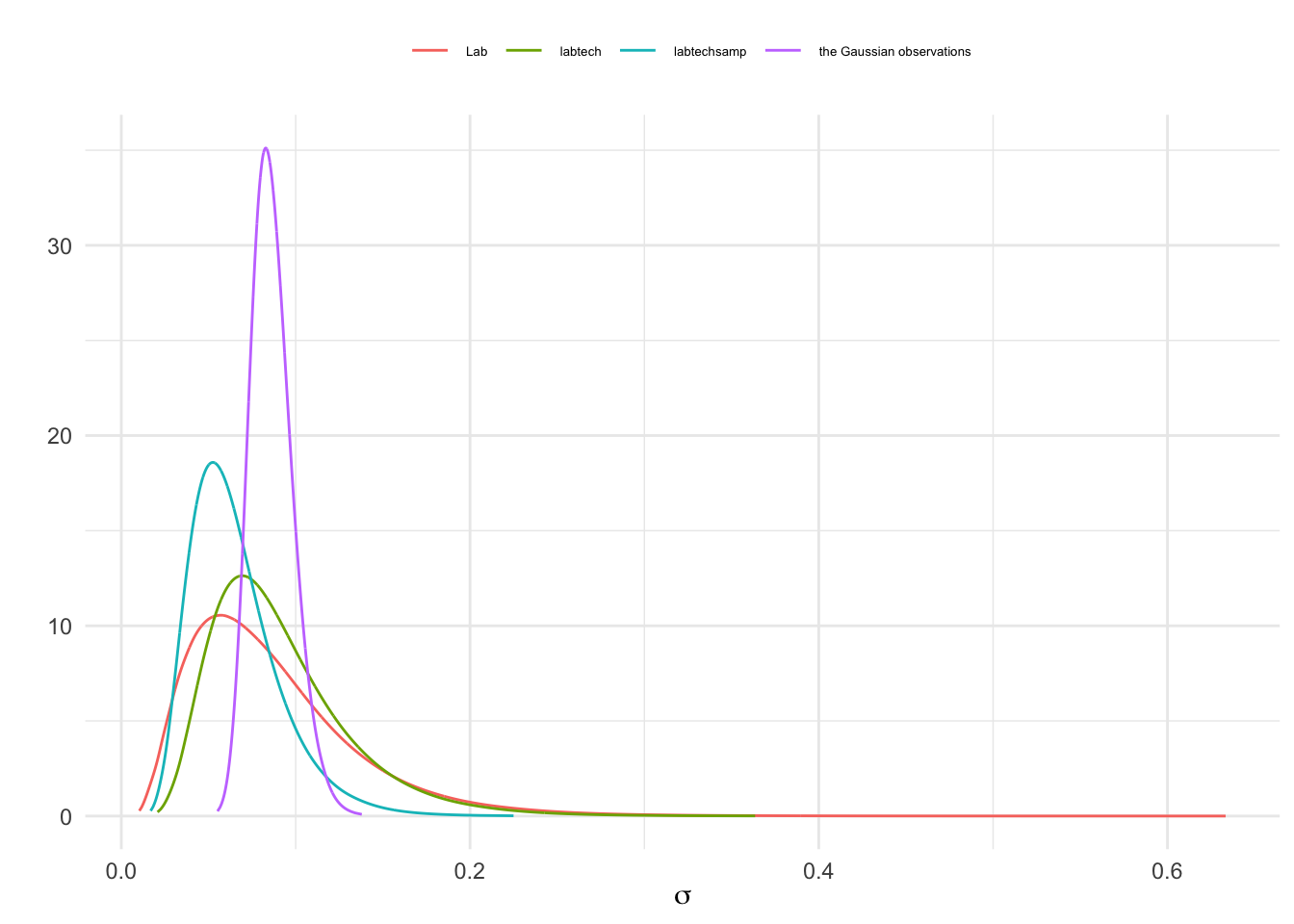

Figura 3.17: Distribución posterior del error de los datos y el error aleatorio

3.8 Conclusiones

Hasta aquí desarrollamos los modelos lineales basados en Anova, esto es, en la integración de factores de clasificación como variables que van a explicar diferencias en la respuesta, como los efectos fijos, o variabilidad extra en los datos, como los efectos aleatorios, a veces incluso con otros predictores de tipo numérico, e incluso interaccionando con ellos.