Unidad 2 Regresión lineal

2.1 Introducción

Una vez presentados los fundamentos de INLA vamos a utilizarlo para trabajar progresivamente desde los modelos más sencillos a los más sofisticados. Empezamos aquí con el modelo de regresión lineal simple, para continuar generalizando con el de regresión lineal múltiple.

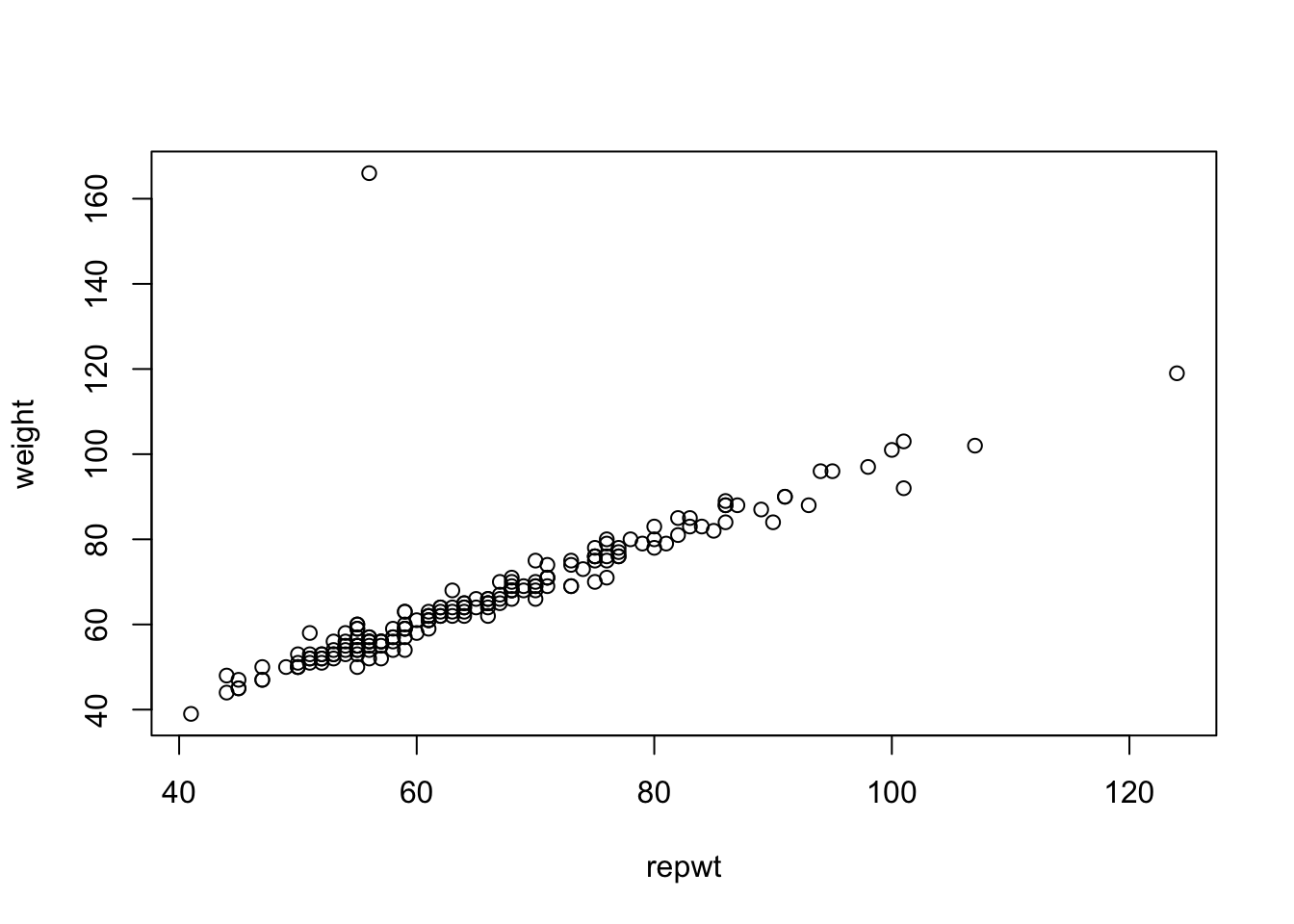
Partimos de la base de datos Davis (en la librería carData), que contiene 200 registros de 5 variables relacionadas con un estudio sobre habituación de hombres y mujeres a la realización de ejercicio físico de forma regular. Las variables que se registraron son sexo, peso y altura (reales y reportados). Vamos a indagar la relación entre el peso real (weight) y el reportado (repwt) a través de un análisis de regresión lineal simple.

data(Davis,package="carData")
plot(weight ~ repwt, data=Davis)

# Excluimos el valor outlier y los NA
davis=Davis %>%
  filter(weight<160) %>%
  slice(which(!is.na(repwt)))

2.2 Variables y relaciones

Entendemos como variable respuesta y=weight, de tipo numérico (continua), y como variable explicativa o covariable, x=repwt, también numérica.

La especificación de respuesta $y$ y predictores $x_1,x_2,...$, en INLA se registra en una fórmula del tipo:

formula= y ~ 1 + x_1 + x_2 +...

en la que podemos prescindir del $1$ que identifica la interceptación, pues el ajuste, por defecto, siempre se resolverá con su estimación, salvo que en su lugar se escriba un ‘-1’.

En nuestro problema tendríamos pues:

formula = weight ~ repwt

A continuación es procedente elegir el modelo sobre la respuesta, o lo que es lo mismo, la verosimilitud.

2.3 Verosimilitud

En principio es razonable asumir normalidad en la respuesta, además de independencia entre todas las observaciones. Así, el modelo propuesto para la respuesta es:

\[(y_i|\mu_i,\sigma^2) \sim N(\mu_i,\sigma^2), i=1,...,n\]

donde y=weight y x=repwt, e $i=1,...,n$ es un subíndice que identifica a cada uno de los registros disponibles en el banco de datos. La media esperada contiene la relación lineal entre covariable y respuesta, $\mu_i=\theta+\beta x_i$, donde $\theta$ es la interceptación de la recta de regresión y $\beta$ el coeficiente que explica la relación lineal entre $x$ e $y$. El vector $(\theta,\beta)$ identifica los efectos latentes, en cuya inferencia posterior estamos interesados, y que están involucrados directamente en la media o predictor lineal. El modelo, o lo que es lo mismo, la verosimilitud, depende también de un parámetro de dispersión $\sigma^2$ sobre el que también querremos inferir.

Veamos cómo especificar este modelo con INLA. La función names(inla.models()) proporciona un listado de todos los tipos de modelos posibles, tanto para los datos (likelihood), para los efectos latentes (latent), los parámetros (prior), y otras opciones que de momento no nos interesan. El listado completo de todas las distribuciones disponibles para cada uno de los tipos de modelos lo obtenemos con el comando inla.list.models(). En particular, si ejecutamos names(inla.models()$likelihood), obtenemos todas las distribuciones disponibles para modelizar los datos.

La distribución gaussian identifica la distribución normal que hemos planteado en nuestro modelo de regresión lineal. Para obtener información sobre cómo está parametrizada y cuáles son las priors por defecto, basta consultar la documentación gaussian con el comando:

# documentación (parametrización y priors) del modelo normal
inla.doc("gaussian")

Para ajustar un modelo sencillo en INLA hay que echar mano de la función inla, en la que introducimos en primer lugar la formula, con la relación entre las variables, a continuación el modelo, en el argumento family, y después el banco de datos sobre el que trabajamos. Si no especificamos el argumento family, la función inla interpreta por defecto la opción gaussian, esto es, normalidad para los datos, de modo que podríamos excluir dicha especificación cuando modelizamos datos normales.

# Asumiendo datos normales
fit=inla(formula,family="gaussian", data)
# equivalente a
fit=inla(formula, data)

Adelantamos pues un paso más en nuestro problema, añadiendo la verosimilitud normal y la base de datos.

# ajuste del modelo
formula = weight ~ 1+ repwt
fit=inla(formula,family="gaussian",data=davis)

2.4 Hiperparámetros

INLA identifica como hiperparámetros todos aquellos parámetros en el modelo que no se corresponden con efectos latentes, esto es, relacionados con el predictor o respuesta esperada. En nuestro modelo, el único hiperparámetro es la varianza $\sigma^2$, sobre la que es preciso especificar una distribución a priori. Para la varianza $\sigma^2$ es habitual asumir una gamma inversa difusa, con media y varianza grandes.

En INLA, en lugar de asignar distribuciones a priori sobre las varianzas, se hace sobre el logaritmo de las precisiones, para facilitar el cálculo del máximo de la log-posterior (obtenida de la log-verosimilitud y la log-prior). Así, asumir una gamma inversa difusa $GaI(\alpha,\beta)$ para la varianza es equivalente a una Gamma difusa $Ga(\alpha,\beta)$ para la precisión $\tau=1/\sigma^2$, y una log-gamma difusa $Log-Gamma(\alpha,\beta)$ para la log-precisión $log(\tau)$.

Por defecto, como ya verificamos en la documentación de la verosimilitud gausiana, (con inla.doc("gaussian")), la distribución a priori por defecto sobre la log-precisión ($\theta_1$ en la ayuda) es la log-gamma difusa $LogGa(1,5\cdot 10^{-5})$, lo que da un valor esperado para la precisión $\tau$ de 20000 y una varianza de $4\cdot 10^8$.

Para modificar la distribución a priori de un parámetro podemos utilizar cualquiera de las distribuciones que ofrece INLA en su listado names(inla.models()$prior) (siempre buscando coherencia con la información sobre el parámetro en cuestión).

Para definir una prior para los parámetros o hiperparámetros en INLA hay que definir los siguientes argumentos:

prior, el nombre de la distribución a priori (para hiperparámetros, alguna de las opciones en names(inla.models()$prior))
param, los valores de los parámetros de la prior
initial, el valor inicial para el hiperparámetro
fixed, variable booleana para decir si el hiperparámetro es fijo o aleatorio.

La modificación la haremos con el argumento control.family=list(hyper=list(...)) en la función inla, al que le proporcionaremos una lista con el nombre de los parámetros (el short name con el que los identifica INLA en la documentación), que apunta a una lista con la distribución (prior) y los parámetros (param) a utilizar.

En nuestro problema, si tenemos información previa sobre la precisión del modelo, reconocida como prec (short name), y queremos especificar una a priori $Ga(1,0.001)$ para la precisión, habremos de utilizar la siguiente sintaxis:

prec.info = list(prior="loggamma", param =c(1,0.001))
fit2=inla(formula,family="gaussian",data=davis,
      control.family = list(hyper = list(prec = prec.info)))

Si nos conformamos con la previa por defecto de INLA, el modelo que estamos asumiendo en nuestro problema de regresión lineal simple será:

\[\begin{eqnarray*} (y_i|\mu_i,\sigma^2) &\sim & N(\mu_i,\sigma^2), i=1,...,n \\ \tau=1/\sigma^2 & \sim & Ga(1,0.00005) \end{eqnarray*}\]

2.5 Efectos fijos

Una variable explicativa entra en el modelo como efecto fijo cuando se piensa que afecta a todas las observaciones del mismo modo, y que su efecto es de interés primario en el estudio.

En un modelo de regresión lineal todos los efectos latentes en el predictor lineal, interceptación y coeficientes de covariables, son efectos fijos. Ante ausencia de información, las priors para los efectos fijos, esto es, ($\theta,\beta$) en nuestro caso, se asumen normales centradas en cero y con varianzas grandes. En INLA la interceptación $\beta$ tiene por defecto una prior gausiana con media y precisión igual a cero (una distribución plana objetiva, que no integra 1), y los coeficientes $\beta$ también tienen una prior gausiana con media cero y precisión igual a 0.001. Estos valores por defecto se pueden consultar con el comando inla.set.control.fixed.default(), que da la siguiente información:

mean=0 y mean.intercept=0 son las medias de la distribución normal para los coeficientes $\beta$ y la interceptación $\theta$ respectivamente
prec=0.001 y prec.intercept=0 son las precisiones respectivas de las normales para $\beta$ y $\theta$.

Con todo, los parámetros de las priors sobre los efectos fijos se pueden modificar a través del argumento control.fixed=list(...) en la función inla, utilizando siempre los nombres que atribuye INLA a los diferentes parámetros e hiperparámetros (short name). Por ejemplo, si queremos modificar la precisión de los efectos fijos para hacerla igual a 0.001 (esto es, varianza 1000), utilizamos la siguiente sintaxis:

formula = weight ~ 1+ repwt
fit=inla(formula,family="gaussian",data=davis,
         control.fixed=list(prec=0.001,prec.intercept=0.001))

Volvemos sobre nuestro ejemplo, y asumiendo las a priori por defecto de INLA tendremos: \[\begin{eqnarray*} (y_i|\theta,\beta,\sigma^2) & \sim & N(\theta+\beta x_i,\sigma^2), i=1,...,n \\ \theta & \sim & N(0,\infty) \\ \beta & \sim & N(0,1000) \\ \tau=1/\sigma^2 & \sim & Ga(1,0.00005) \end{eqnarray*}\]

2.6 Resultados

Para mostrar una descriptiva de los resultados del ajuste obtenido con fit=inla(...), utilizamos la sintaxis siguiente:

summary(fit) proporciona una descriptiva del ajuste
names(fit$marginals.fixed) lista los nombres de todos los efectos fijos
fit$summary.fixed resume la inferencia posterior sobre los efectos fijos
names(fit$marginals.hyperpar) lista los nombres de todos los hiperparámetros
fit$summary.hyperpar da un resumen de la inferencia posterior de los parámetros e hiperparámetros
fit$summary.fitted.values resume la inferencia posterior sobre los valores ajustados
fit$mlik da la estimación de la log-verosimilitud marginal, útil para evaluar y comparar modelos.

Veamos los resultados para nuestro problema de regresión.

# ajuste del modelo 
formula = weight ~ 1+ repwt
fit=inla(formula,family="gaussian",data=davis)
summary(fit)
#> 
#> Call:
#>    c("inla.core(formula = formula, family = family, 
#>    contrasts = contrasts, ", " data = data, quantiles = 
#>    quantiles, E = E, offset = offset, ", " scale = 
#>    scale, weights = weights, Ntrials = Ntrials, strata = 
#>    strata, ", " lp.scale = lp.scale, link.covariates = 
#>    link.covariates, verbose = verbose, ", " lincomb = 
#>    lincomb, selection = selection, control.compute = 
#>    control.compute, ", " control.predictor = 
#>    control.predictor, control.family = control.family, 
#>    ", " control.inla = control.inla, control.fixed = 
#>    control.fixed, ", " control.mode = control.mode, 
#>    control.expert = control.expert, ", " control.hazard 
#>    = control.hazard, control.lincomb = control.lincomb, 
#>    ", " control.update = control.update, 
#>    control.lp.scale = control.lp.scale, ", " 
#>    control.pardiso = control.pardiso, only.hyperparam = 
#>    only.hyperparam, ", " inla.call = inla.call, inla.arg 
#>    = inla.arg, num.threads = num.threads, ", " 
#>    blas.num.threads = blas.num.threads, keep = keep, 
#>    working.directory = working.directory, ", " silent = 
#>    silent, inla.mode = inla.mode, safe = FALSE, debug = 
#>    debug, ", " .parent.frame = .parent.frame)") 
#> Time used:
#>     Pre = 2.41, Running = 0.192, Post = 0.019, Total = 2.62 
#> Fixed effects:
#>              mean    sd 0.025quant 0.5quant 0.975quant mode
#> (Intercept) 2.734 0.814      1.135    2.734      4.333   NA
#> repwt       0.958 0.012      0.935    0.958      0.982   NA
#>             kld
#> (Intercept)   0
#> repwt         0
#> 
#> Model hyperparameters:
#>                                          mean    sd
#> Precision for the Gaussian observations 0.199 0.021
#>                                         0.025quant 0.5quant
#> Precision for the Gaussian observations      0.161    0.198
#>                                         0.975quant mode
#> Precision for the Gaussian observations      0.242   NA
#> 
#> Marginal log-Likelihood:  -426.73 
#>  is computed 
#> Posterior summaries for the linear predictor and the fitted values are computed
#> (Posterior marginals needs also 'control.compute=list(return.marginals.predictor=TRUE)')
fit$mlik
#>                                            [,1]
#> log marginal-likelihood (integration) -426.7385
#> log marginal-likelihood (Gaussian)    -426.7323

Obtenemos pues la salida con un descriptivo de la distribución posterior para los efectos fijos interceptación, $\theta$, y el coeficiente del regresor repwt, $\beta$, con la media, desviación típica y cuantiles con los que podemos evaluar la región creíble al 95%.

También muestra a continuación una tabla con los descriptivos de la distribución posterior para la precisión $\tau=1/\sigma^2$ de los datos.

Si queremos obtener los nombres con los que INLA reconoce los efectos fijos (interceptación y coeficiente del regresor) e hiperparámetros (precisión de los datos), llamamos a

names(fit$marginals.fixed)
#> [1] "(Intercept)" "repwt"
names(fit$marginals.hyperpar)
#> [1] "Precision for the Gaussian observations"

Y podemos pedir descriptivos específicos de las distribuciones de los efectos fijos y de los hiperparámetros.

# descriptivos efectos fijos
fit$summary.fixed
#>                  mean         sd 0.025quant  0.5quant
#> (Intercept) 2.7338111 0.81438483  1.1348914 2.7338110
#> repwt       0.9583742 0.01213663  0.9345457 0.9583742
#>             0.975quant mode          kld
#> (Intercept)  4.3327314   NA 6.303549e-10
#> repwt        0.9822026   NA 6.306970e-10
# descriptivos varianza
fit$summary.hyperpar
#>                                              mean
#> Precision for the Gaussian observations 0.1990956
#>                                                 sd
#> Precision for the Gaussian observations 0.02088519
#>                                         0.025quant
#> Precision for the Gaussian observations  0.1608475
#>                                          0.5quant
#> Precision for the Gaussian observations 0.1983642
#>                                         0.975quant mode
#> Precision for the Gaussian observations  0.2418474   NA
# medias de los efectos fijos
fit$summary.fixed$mean
#> [1] 2.7338111 0.9583742
# descriptivos primer efecto fijo
fit$summary.fixed[1,]
#>                 mean        sd 0.025quant 0.5quant
#> (Intercept) 2.733811 0.8143848   1.134891 2.733811
#>             0.975quant mode          kld
#> (Intercept)   4.332731   NA 6.303549e-10

Para describir la marginal posterior sobre cada uno de los datos ajustados:

head(fit$summary.fitted.values)
#>                          mean        sd 0.025quant 0.5quant
#> fitted.Predictor.001 76.52862 0.2162698   76.10405 76.52862
#> fitted.Predictor.002 51.61089 0.2441494   51.13159 51.61089
#> fitted.Predictor.003 54.48602 0.2190068   54.05607 54.48602
#> fitted.Predictor.004 69.82000 0.1750354   69.47638 69.82000
#> fitted.Predictor.005 59.27789 0.1856012   58.91352 59.27789
#> fitted.Predictor.006 75.57025 0.2087672   75.16040 75.57025
#>                      0.975quant mode
#> fitted.Predictor.001   76.95319   NA
#> fitted.Predictor.002   52.09020   NA
#> fitted.Predictor.003   54.91596   NA
#> fitted.Predictor.004   70.16362   NA
#> fitted.Predictor.005   59.64225   NA
#> fitted.Predictor.006   75.98009   NA

Si queremos hacer un análisis de sensibilidad sobre las distribuciones a priori, reajustamos el modelo con otras priors y comparamos los resultados.

# ajuste del modelo 
formula = weight ~ 1+ repwt
fit2=inla(formula,family="gaussian",data=davis,
         control.fixed = list(mean.intercept = 100, 
                                 prec.intercept = 0.001,
                                 prec = 0.001), 
            control.family = list(hyper = list(
              prec = list(prior="loggamma", param =c(1,0.001)))))
fit2$summary.fixed
#>                  mean         sd 0.025quant  0.5quant
#> (Intercept) 2.7982510 0.81395827  1.2011565 2.7979109
#> repwt       0.9574342 0.01213043  0.9336043 0.9574392
#>             0.975quant mode          kld
#> (Intercept)   4.397273   NA 6.167716e-10
#> repwt         0.981236   NA 6.162515e-10
fit2$summary.hyperpar
#>                                              mean
#> Precision for the Gaussian observations 0.1990551
#>                                                 sd
#> Precision for the Gaussian observations 0.02087866
#>                                         0.025quant
#> Precision for the Gaussian observations  0.1603498
#>                                          0.5quant
#> Precision for the Gaussian observations 0.1983172
#>                                         0.975quant mode
#> Precision for the Gaussian observations  0.2418039   NA

2.7 Distribuciones posteriores

Para obtener la distribución marginal de los valores ajustados y predichos necesitamos incorporar a la función inla el argumento control.compute=list(return.marginals.predictor=TRUE).

Tras conseguir un ajuste con inla, podemos acceder a todas las distribuciones marginales posteriores y predictivas a través de:

fit$marginals.fixed da las distribuciones posteriores marginales de los efectos fijos
fit$marginals.fixed$xx da la distribución del efecto fijo xx, y también se puede seleccionar con su ordinal en el conjunto de efectos fijos fit$marginals.fixed[[i]]
fit.marginals.hyperpar da las distribuciones posteriores marginales de los parámetros e hiperparámetros
fit$marginals.fitted.values da las distribuciones posteriores marginales para los valores ajustados

Con estas distribuciones, reconocidas como marginal, podemos hacer cálculos y gráficos de interés a través de estas funciones que operan sobre las distribuciones y que podemos consultar con ?inla.marginal:

inla.dmarginal(x, marginal, ...) da la densidad en x
inla.pmarginal(q, marginal, ...) da las probabilidades o función de distribución
inla.qmarginal(p, marginal,...) da los cuantiles
inla.rmarginal(n, marginal) permite obtener $n$ simulaciones
inla.hpdmarginal(p, marginal,...) da la región HPD
inla.smarginal(marginal, ...) da un suavizado con splines de la distribución marginal
inla.emarginal(fun, marginal, ...) calcula el valor esperado de una función
inla.mmarginal(marginal,...) calcula la moda posterior
inla.tmarginal(fun, marginal,...) transforma la distribución marginal de una función del parámetro
inla.zmarginal(marginal,...) calcula descriptivos de la marginal.

Veamos algunos ejemplos sobre nuestro problema. Vamos a mostrar a continuación, en un único gráfico, las distribuciones posteriores de los efectos fijos y el parámetro de dispersión de los datos $, con líneas verticales que marquen el valor esperado posterior (en azul) y el HPD95% en rojo.

# library(gridExtra)
# library(ggplot2)

g=list() # lista en que almacenamos los gráficos con d.posteriores
# Efectos fijos
names.fixed=names(fit$marginals.fixed)
n.fixed=length(names.fixed)
names=c(expression(theta),expression(beta))
for (i in 1:n.fixed){
 g[[i]] = ggplot(as.data.frame(fit$marginals.fixed[[i]])) + 
  geom_line(aes(x = x, y = y)) +
  labs(x=names[i],y="")+
   geom_vline(xintercept=inla.hpdmarginal(0.95,fit$marginals.fixed[[i]]),
             linetype="dashed",color="red")+
  geom_vline(xintercept=inla.emarginal(function(x) x,fit$marginals.fixed[[i]]),
             linetype="dashed",color="blue")
}


# Parámetros
g[[3]]= ggplot(as.data.frame(fit$marginals.hyperpar[[1]])) + 
  geom_line(aes(x = x, y = y)) +
  labs(x=expression(tau),y="")+
  geom_vline(xintercept=inla.hpdmarginal(0.95,fit$marginals.hyperpar[[1]]),
             linetype="dashed",color="red")+
  geom_vline(xintercept=inla.emarginal(function(x) x,fit$marginals.hyperpar[[1]]),
             linetype="dashed",color="blue")

# Transformamos la posterior en tau para obtener la posterior de sigma
sigma.post=inla.tmarginal(function(tau) tau^(-1/2),
  fit$marginals.hyperpar[[1]])
# y la pintamos
g[[4]]= ggplot(as.data.frame(sigma.post)) + 
  geom_line(aes(x = x, y = y)) +
  labs(x=expression(sigma),y="")+
  geom_vline(xintercept=inla.hpdmarginal(0.95,sigma.post),
             linetype="dashed",color="red")+
  geom_vline(xintercept=inla.emarginal(function(x) x,sigma.post),
             linetype="dashed",color="blue")

library(gridExtra)
grid.arrange(g[[1]],g[[2]],g[[3]],g[[4]],ncol=2)

Si queremos la distribución posterior de alguna de las medias $\mu_i=\theta+ \beta x_i$, necesitamos añadir el argumento control.compute=list(return.marginals.predictor=TRUE) en inla. Así podremos representar, por ejemplo, la distribución posterior sobre el peso esperado para el individuo que aparece en el registro 1 de la base de datos, $\mu_1=\theta+\beta x_1$:

fit=inla(formula,family="gaussian",data=davis,
         control.compute=list(return.marginals.predictor=TRUE))
ggplot(as.data.frame(fit$marginals.fitted.values[[1]]),aes(x=x,y=y))+
  geom_line()+
  labs(x=expression(mu[1]),y="D.Posterior")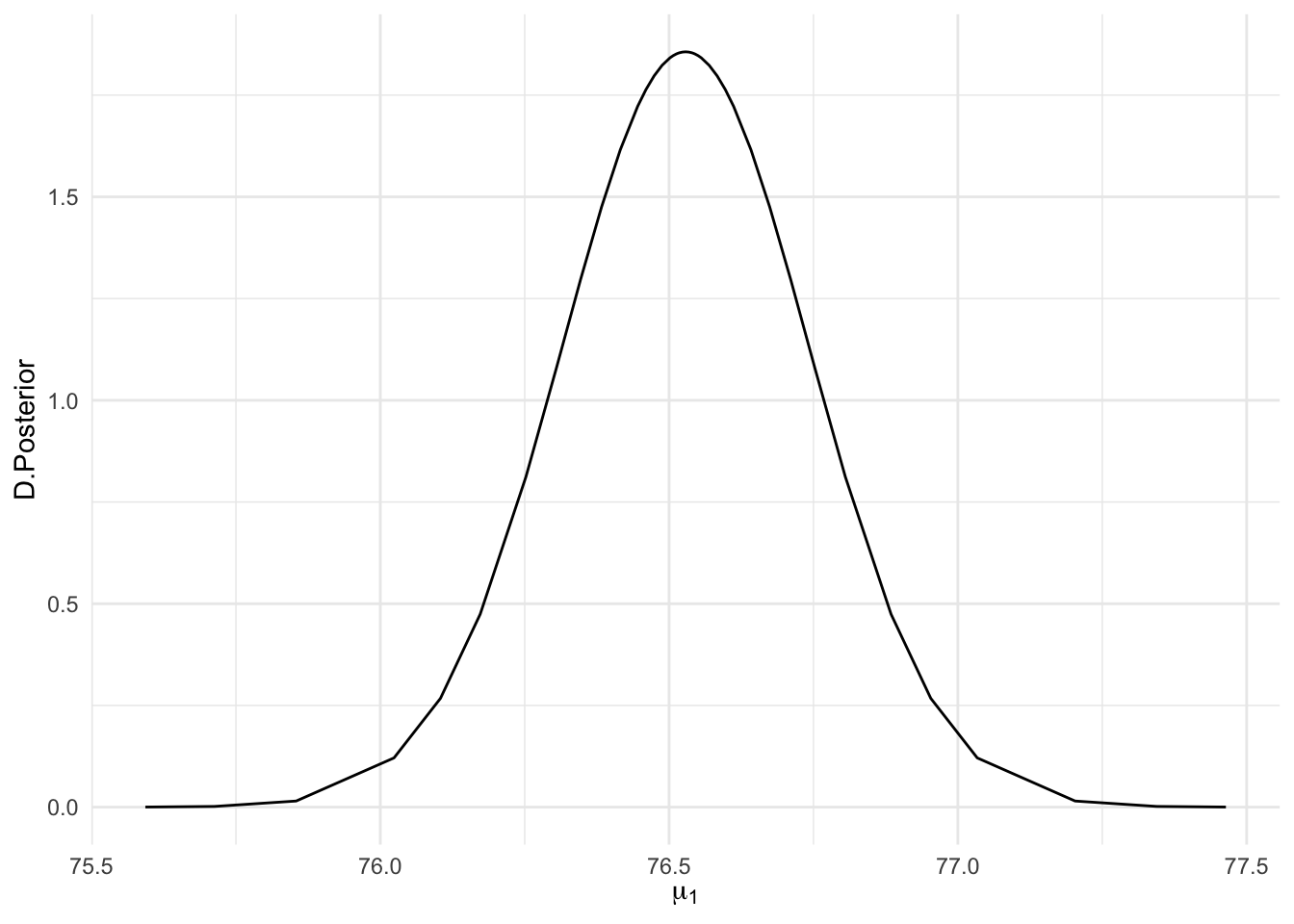

2.8 Simulación de la posterior

Cuando queremos inferir sobre funciones de los efectos latentes e hiperparámetros que no proporciona INLA por defecto , podemos recurrir a simular de las distribuciones posteriores de los efectos involucrados, y con ellas evaluar la función que nos interesa, para conseguir una muestra de su distribución posterior.

Para ello es preciso que al ajustar el modelo con inla hayamos incluido el argumento control.compute=list(config=TRUE).

Para obtener simulaciones de las correspondientes distribuciones posteriores, utilizamos las funciones:

inla.posterior.sample(n, fit,selection), para simular los efectos latentes, donde $n$ es el número de simulaciones pretendido, fit es el ajuste obtenido con inla y selection es una lista con el nombre de las componentes (efectos latentes) a simular.
inla.hyperpar.sample(n,fit,improve.marginals=TRUE) para simular de parámetros e hiperparámetros.

Para describir las distribuciones de los nuevos parámetros que queremos evaluar con dichas simulaciones, utilizaremos:

inla.posterior.eval() para funciones sobre los efectos fijos
inla.hyperpar.eval() para funciones sobre los hiperparámetros

Imaginemos que queremos obtener la distribución posterior de $(\theta+\beta \cdot 50)$, que correspondería con el peso real de un sujeto que ha declarado un peso de 50kg. Hemos de simular pues, de las distribuciones posteriores de $\theta$ y de $\beta$, para luego aplicar la función correspondiente sobre las simulaciones y obtener una muestra posterior de $\theta+\beta\cdot 50$.

# reajustamos para poder simular de las posterioris
fit <- inla(formula, data = davis,
  control.compute = list(config = TRUE))
# simulamos especificando los parámetros en los que tenemos interés
sims = inla.posterior.sample(100, fit, selection = list("(Intercept)"=1,repwt = 1))

Esto nos devuelve una lista de la dimensión del número de simulaciones (cada simulación en un elemento de la lista), y en cada uno de los elementos tenemos los valores simulados de los hiperparámetros (hyper), de los efectos latentes (latent)

length(sims)
#> [1] 100
names(sims[[1]])
#> [1] "hyperpar" "latent"   "logdens"
sims[[1]]$hyperpar
#> Precision for the Gaussian observations 
#>                               0.2507863
sims[[1]]$latent
#>                sample:1
#> (Intercept):1 2.0338024
#> repwt:1       0.9690668

y la log-densidad de la posterior en esos valores (logdens)

 sims[[1]]$logdens
#> $hyperpar
#> [1] 0.2088468
#> 
#> $latent
#> [1] 1014.145
#> 
#> $joint
#> [1] 1014.354

Ahora con la función inla.posterior.sample.eval, dado que nuestra función depende de efectos fijos (latentes), $(\theta,\beta)$, evaluamos la operación pretendida, y con descriptivos gráficos y numéricos de las simulaciones, podemos aproximar los descriptivos de la distribución posterior.

peso_real=inla.posterior.sample.eval(function(...) {(Intercept)+repwt*50},sims)
peso_real
#>        sample:1 sample:2 sample:3 sample:4 sample:5
#> fun[1] 50.48714 50.96914 50.88513 50.55123 50.43433
#>        sample:6 sample:7 sample:8 sample:9 sample:10
#> fun[1] 50.95626 50.24634 50.67908 50.79885  50.40503
#>        sample:11 sample:12 sample:13 sample:14 sample:15
#> fun[1]  50.85233  50.76262  50.49461  50.12846  50.02194
#>        sample:16 sample:17 sample:18 sample:19 sample:20
#> fun[1]  50.71335   50.6657  50.22515  50.53359  50.83593
#>        sample:21 sample:22 sample:23 sample:24 sample:25
#> fun[1]  50.81653  50.53385  50.37291  50.78633  50.55807
#>        sample:26 sample:27 sample:28 sample:29 sample:30
#> fun[1]  51.11283  50.99547  50.99155  50.53261   50.9319
#>        sample:31 sample:32 sample:33 sample:34 sample:35
#> fun[1]  50.60077  50.75911  50.88658  50.96568  50.42115
#>        sample:36 sample:37 sample:38 sample:39 sample:40
#> fun[1]  51.25975  50.41521  50.30793  50.61346  50.87203
#>        sample:41 sample:42 sample:43 sample:44 sample:45
#> fun[1]  50.58164    50.644  50.48652  50.15448  50.39808
#>        sample:46 sample:47 sample:48 sample:49 sample:50
#> fun[1]  51.04667  50.79767  50.36373  50.89159  50.82715
#>        sample:51 sample:52 sample:53 sample:54 sample:55
#> fun[1]  50.46695  50.73265  50.47238  49.88365  50.42799
#>        sample:56 sample:57 sample:58 sample:59 sample:60
#> fun[1]  50.84092  50.92923  50.89597  50.94903  50.56953
#>        sample:61 sample:62 sample:63 sample:64 sample:65
#> fun[1]  51.06785  50.44609  50.40124  50.91221  50.37128
#>        sample:66 sample:67 sample:68 sample:69 sample:70
#> fun[1]  50.98535  50.97738  50.76141  50.58924   50.6614
#>        sample:71 sample:72 sample:73 sample:74 sample:75
#> fun[1]  50.41653  50.95951  50.81905  50.69168  50.63137
#>        sample:76 sample:77 sample:78 sample:79 sample:80
#> fun[1]  50.80738  50.37161  50.52499  50.32938  50.64523
#>        sample:81 sample:82 sample:83 sample:84 sample:85
#> fun[1]  50.61906  50.46631  50.31782  50.39405   50.6167
#>        sample:86 sample:87 sample:88 sample:89 sample:90
#> fun[1]  50.41176  51.17623  50.90767  50.71781   50.4825
#>        sample:91 sample:92 sample:93 sample:94 sample:95
#> fun[1]  50.45913  50.39679   50.9806  50.63767  50.55077
#>        sample:96 sample:97 sample:98 sample:99 sample:100
#> fun[1]  50.84225  50.97529  50.53797  50.29124   50.43499
pred=data.frame(peso=as.vector(peso_real))
summary(pred)
#>       peso      
#>  Min.   :49.88  
#>  1st Qu.:50.43  
#>  Median :50.63  
#>  Mean   :50.64  
#>  3rd Qu.:50.86  
#>  Max.   :51.26
ggplot(pred,aes(x=peso))+
  geom_histogram(aes(y=..density..), colour="black", fill="white")+
  geom_density(alpha=.2, fill="#80E7F5") 
#> `stat_bin()` using `bins = 30`. Pick better value with
#> `binwidth`.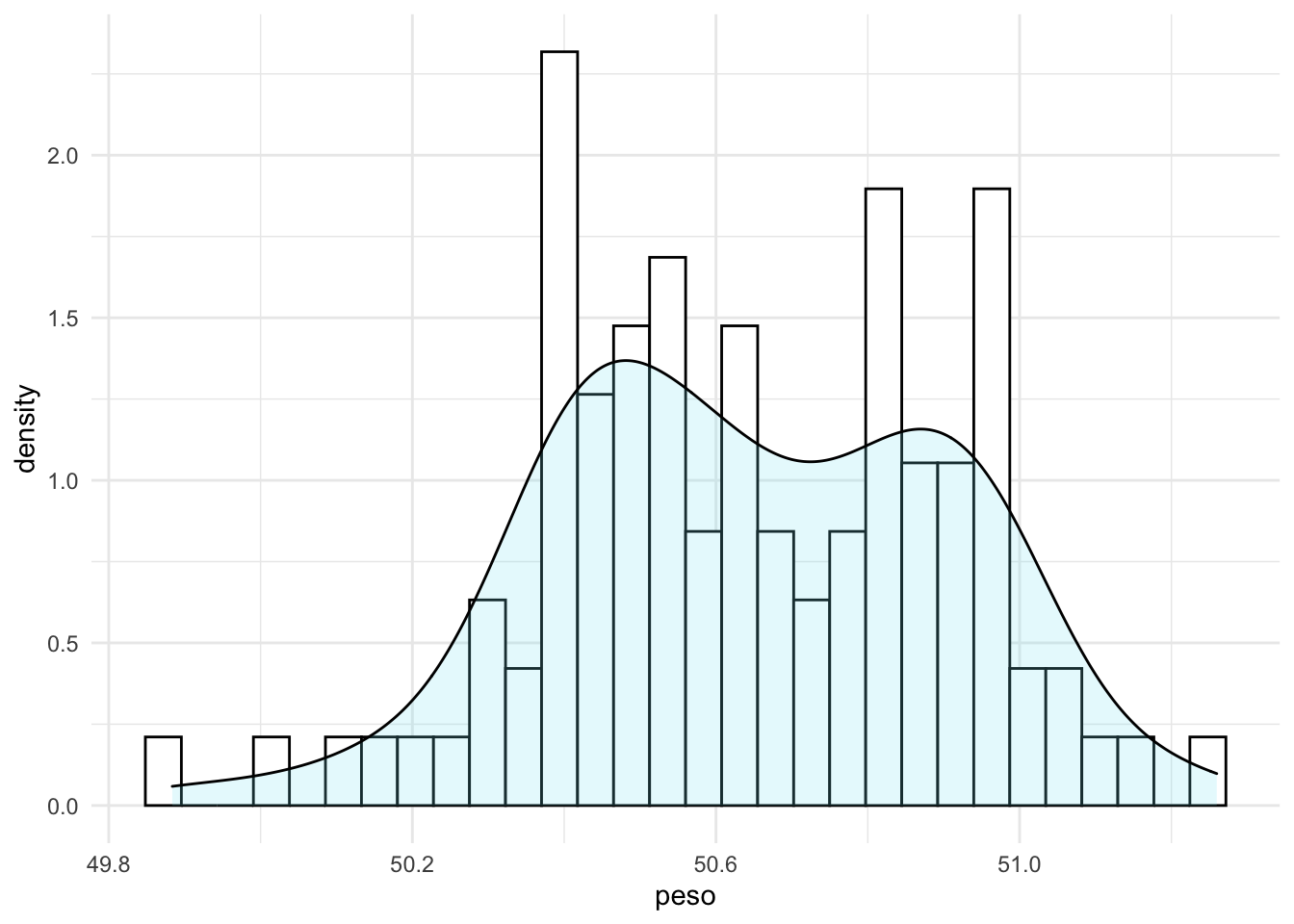

2.9 Regresión lineal múltiple con INLA

Vemos a continuación cómo se trabaja la regresión múltiple con INLA, simplemente añadiendo más predictores.

El modelo de regresión asume una distribución normal para los datos, datos los efectos latentes (todos los relacionados con el valor esperado o predictor lineal) y el resto de parámetros o hiperparámetros del modelo (en nuestro caso la varianza de los datos).

Si tenemos $n$ observaciones \[ (y_i|\mu_i,\sigma^2) \sim N(\mu_i,\sigma^2), \ \ i=1,...n\] donde $\mu_i$ representa la media y $\sigma^2$ la varianza de los datos. \[E(y_i|\mu_i,\sigma^2)=\mu_i, \ Var(y_i|\mu_i,\sigma^2)=\sigma^2\] Si tenemos varios regresores $x_1,x_2,...,x_J$, la media $\mu_i$ coincide con el predictor lineal $\eta_i$ que se construye a partir de una combinación lineal de los predictores: \[\mu_i=\eta_i=\theta+ \sum_{j=1}^J \beta_j x_{ij}\] Nos queda a continuación especificar las distribuciones a priori sobre el vector de efectos latentes, en nuestro caso efectos fijos, $(\theta,\beta_1,...,\beta_J)$, y sobre el parámetro de dispersión o hiperparámetro $\sigma^2$.

Cuando no tenemos información previa especificamos distribuciones difusas (vagas) sobre los parámetros. En INLA por defecto tendremos:

\[\begin{eqnarray*} \theta &\sim& N(0,\sigma_{\theta}^2) \\ \beta_j &\sim& N(0,\sigma_{\beta}^2) \\ log(\tau=1/\sigma^2) &\sim& Log-Ga(1,0.00005) \end{eqnarray*}\] con $\sigma_{\theta}^2=\infty$ y $\sigma_{\beta}^2=1000$.

Ejemplificamos el análisis de regresión lineal múltiple sobre la base de datos usair, en la librería brinla. Esta BD contiene datos recopilados para investigar los factores determinantes de la polución, utilizando el nivel de SO2 como variable dependiente y las restantes como variables explicativas potenciales. Las relaciones entre las variables que incluye se muestra en la Figura 2.1 a continuación.

data(usair, package = "brinla")
library(GGally) # contiene la función de graficado 'ggpairs'
pairs.chart <- ggpairs(usair, lower = list(continuous = "cor"), 
                       upper = list(continuous = "points", combo = "dot"))
ggplot2::theme(axis.text = element_text(size = 6)) 
#> List of 1
#>  $ axis.text:List of 11
#>   ..$ family       : NULL
#>   ..$ face         : NULL
#>   ..$ colour       : NULL
#>   ..$ size         : num 6
#>   ..$ hjust        : NULL
#>   ..$ vjust        : NULL
#>   ..$ angle        : NULL
#>   ..$ lineheight   : NULL
#>   ..$ margin       : NULL
#>   ..$ debug        : NULL
#>   ..$ inherit.blank: logi FALSE
#>   ..- attr(*, "class")= chr [1:2] "element_text" "element"
#>  - attr(*, "class")= chr [1:2] "theme" "gg"
#>  - attr(*, "complete")= logi FALSE
#>  - attr(*, "validate")= logi TRUE
pairs.chart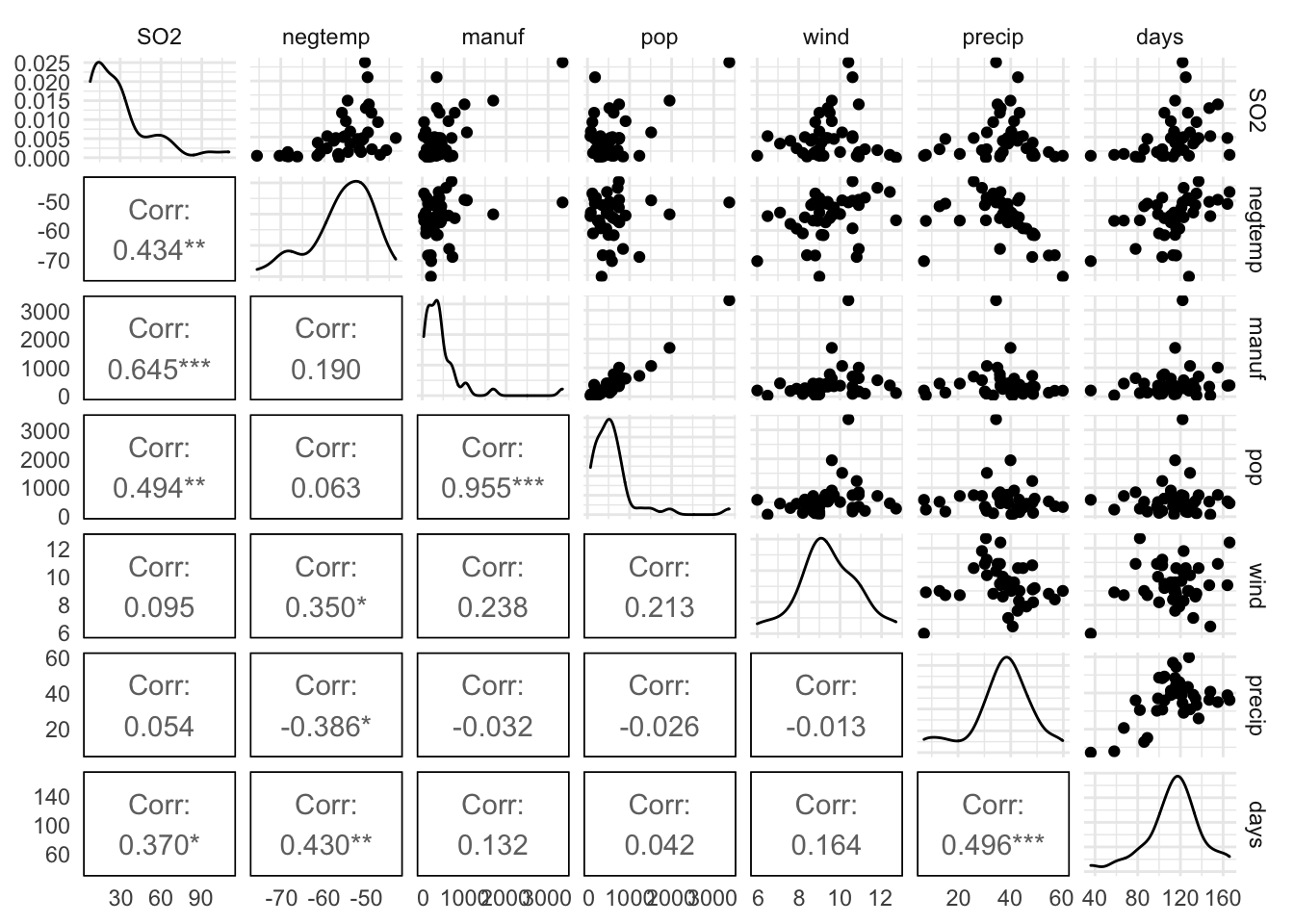

Figura 2.1: Relaciones entre variables en la base de datos usair(brinla).

Apreciamos ya en el gráfico una correlación positiva muy alta entre las variables pop y manuf, y relevante para negtemp y days y también para precip y days, lo que posteriormente condicionará la selección de variables.

2.9.1 Selección de variables

Cuando trabajamos con más de una variable predictora en regresión lineal (realmente en cualquier modelo) surge un problema adicional, que es la selección de variables, o selección del mejor modelo de predicción. Esto se resuelve en INLA utilizando diversos criterios de selección entre los que destacamos:

la verosimilitud marginal (valor de la log-verosimilitud): mlik; al cambiarle el signo tendremos -(log-likelihood)
el criterio de información de la deviance (DIC): dic
el criterio de información bayesiana ampliado (WAIC): waic
la transformada integral predictiva (PIT): cpo

El procedimiento a utilizar para la selección del modelo (de variables) es el siguiente:

ajustar todos los modelos resultantes de todas las combinaciones posibles de predictoras,
calcular los índices de selección para cada uno de ellos
proceder con la selección en base a dichos valores.

Siempre se prefieren modelos con los valores más bajos para estos criterios y se descartan los que proporcionan valores más altos. Cuando no es el mismo modelo el que proporciona el valor mínimo en estos criterios, habremos de optar por alguno de ellos.

Por defecto, al ajustar un modelo con inla, nos devuelve la log-verosimilitud marginal (accesible con fit$mlik si el ajuste se guardó en el objeto fit). Para obtener las otras medidas de selección, hemos de incluir como argumento de la función inla, la opción control.compute = list(dic = TRUE, waic = TRUE)). Los valores por defecto de control.compute los podemos consultar ejecutando el comando inla.set.control.compute.default().

Vayamos pues con el ajuste del modelo de regresión con todas las variables. Recordemos que si no especificamos el argumento family, interpreta por defecto la opción gaussian, esto es, normalidad para los datos. Así ajustamos el modelo y obtenemos las siguientes inferencias sobre los efectos fijos.

formula <-  SO2 ~ negtemp + manuf + wind + precip + days
fit= inla(formula, data = usair, 
          control.compute = list(dic = TRUE, waic = TRUE))
#summary(fit)
round(fit$summary.fixed,3)
#>                mean     sd 0.025quant 0.5quant 0.975quant
#> (Intercept) 135.487 49.861     37.151  135.495    233.780
#> negtemp       1.769  0.634      0.518    1.769      3.020
#> manuf         0.026  0.005      0.017    0.026      0.035
#> wind         -3.723  1.935     -7.536   -3.723      0.093
#> precip        0.625  0.387     -0.139    0.625      1.388
#> days         -0.057  0.174     -0.400   -0.057      0.287
#>             mode kld
#> (Intercept)   NA   0
#> negtemp       NA   0
#> manuf         NA   0
#> wind          NA   0
#> precip        NA   0
#> days          NA   0

La inferencia posterior sobre la desviación típica de los datos, $\sigma$, la resolvemos con sus descriptivos.

sigma.post= inla.tmarginal(function(tau) tau^(-1/2),
                           fit$marginals.hyperpar[[1]])
inla.zmarginal(sigma.post)
#> Mean            15.6813 
#> Stdev           1.84661 
#> Quantile  0.025 12.5832 
#> Quantile  0.25  14.3546 
#> Quantile  0.5   15.4971 
#> Quantile  0.75  16.8026 
#> Quantile  0.975 19.8219

Para seleccionar las variables relevantes seguimos el procedimiento descrito anteriormente. Añadimos también el ajuste del modelo de regresión frecuentista, para el que calculamos como criterio de bondad de ajuste el AIC.

# variables en la bd
vars=names(usair)[-1] # variables predictoras (excluye v.dpte)
nvars=length(vars) # nº variables predictoras

# Truco para concatenar todos los modelos posibles en una fórmula (de Faraway)
listcombo <- unlist(sapply(1:nvars,
                           function(x) combn(nvars, x, simplify=FALSE)),
                    recursive=FALSE)
predterms <- lapply(listcombo, 
                    function(x) paste(vars[x],collapse="+"))
nmodels <- length(listcombo)
coefm <- matrix(NA,length(listcombo),4,
                dimnames=list(predterms,c("AIC","DIC","WAIC","MLIK")))

# Ajuste de todos los modelos posibles
for(i in 1:nmodels){
  formula <- as.formula(paste("SO2 ~ ",predterms[[i]]))
  # modelo frecuentista
  lmi <- lm(formula, data=usair)
  # modelo bayesiano
  result <- inla(formula, family="gaussian", data=usair, control.compute=list(dic=TRUE, waic=TRUE))
  coefm[i,1] <- AIC(lmi)
  coefm[i,2] <- result$dic$dic
  coefm[i,3] <- result$waic$waic
  coefm[i,4] <- -result$mlik[1]
}

Ya solo resta comparar los resultados, respecto de cada uno de los criterios, para seleccionar con qué variables nos quedamos, y por lo tanto con qué modelo de predicción. Basta con encontrar el modelo que proporciona el mínimo valor en cada uno de los criterios.

gana.aic = predterms[which.min(coefm[,1])]
gana.dic = predterms[which.min(coefm[,2])]
gana.waic = predterms[which.min(coefm[,3])]
gana.mlik = predterms[which.min(coefm[,4])]
gana.aic;gana.dic
#> [[1]]
#> [1] "negtemp+manuf+pop+wind+precip"
#> [[1]]
#> [1] "negtemp+manuf+pop+wind+precip"
gana.waic;gana.mlik
#> [[1]]
#> [1] "negtemp+manuf+pop+wind+precip"
#> [[1]]
#> [1] "manuf"

Concluimos pues que, tanto el criterio AIC en el modelo de regresión frecuentista, como los criterios DIC y WAIC en el modelo de regresión bayesiano, proporcionan el mejor ajuste. Este mejor modelo incluye como predictores las variables ‘negtemp+manuf+pop+wind+precip’. Reajustamos el modelo con estas variables para derivar las inferencias y predicciones.

Las inferencias sobre los efectos fijos y la precisión de los datos se muestran a continuación.

formula=SO2 ~ negtemp+manuf+pop+wind+precip
fit=inla(formula, family="gaussian", data=usair, control.compute=list(dic=TRUE, waic=TRUE))
fit$summary.fixed
#>                     mean          sd   0.025quant
#> (Intercept) 100.01542077 30.13189996 40.595824939
#> negtemp       1.12026887  0.41418629  0.303552452
#> manuf         0.06489630  0.01548657  0.034362250
#> pop          -0.03934768  0.01488029 -0.068687883
#> wind         -3.07256361  1.75616870 -6.534354955
#> precip        0.41922312  0.21542102 -0.005537739
#>                 0.5quant   0.975quant mode          kld
#> (Intercept) 100.01892454 159.41499344   NA 1.154246e-08
#> negtemp       1.12029498   1.93683617   NA 1.157203e-08
#> manuf         0.06489607   0.09543164   NA 1.158379e-08
#> pop          -0.03934735  -0.01000932   NA 1.158317e-08
#> wind         -3.07281490   0.39066413   NA 1.151620e-08
#> precip        0.41922947   0.84394766   NA 1.158140e-08
fit$summary.hyperpar
#>                                                mean
#> Precision for the Gaussian observations 0.005066401
#>                                                  sd
#> Precision for the Gaussian observations 0.001178478
#>                                         0.025quant
#> Precision for the Gaussian observations 0.00303683
#>                                           0.5quant
#> Precision for the Gaussian observations 0.00497558
#>                                          0.975quant mode
#> Precision for the Gaussian observations 0.007614574   NA

Y en la Figura 2.2 se muestran las distribuciones posteriores de todos los efectos latentes (efectos fijos) en el modelo: interceptación y coeficientes de los regresores.

nfixed=length(fit$names.fixed)
g=list()
for(i in 1:nfixed){
  g[[i]]=ggplot(as.data.frame(fit$marginals.fixed[[i]])) + 
    geom_line(aes(x = x, y = y)) +
    labs(x=fit$names.fixed[i],y="")+
    geom_vline(xintercept=inla.hpdmarginal(0.95,fit$marginals.fixed[[i]]),
               linetype="dashed",color="red")+
    geom_vline(xintercept=inla.emarginal(function(x) x,fit$marginals.fixed[[i]]),
               linetype="dashed",color="blue")
}
grid.arrange(g[[1]],g[[2]],g[[3]],g[[4]],g[[5]],g[[6]],ncol=2)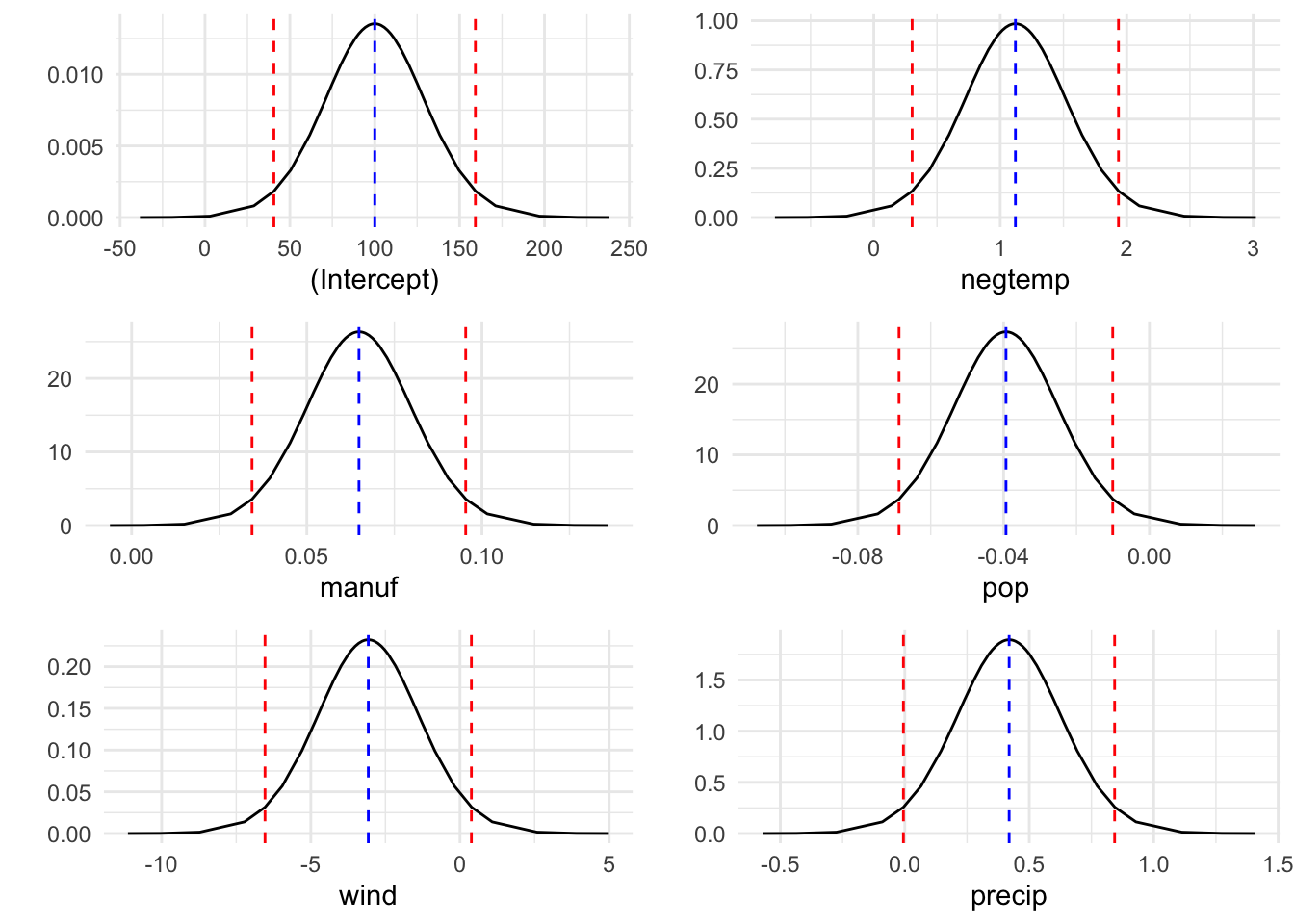

Figura 2.2: Distribuciones posteriores de los efectos latentes.

2.9.2 Predicción de medias

Por último, si queremos predecir la respuesta esperada para ciertos valores de las variables explicativas, no necesariamente existentes en la base de datos, utilizamos el argumento control.predictor en la función inla, especificando en una lista los valores a predecir. Veamos cómo hacerlo con inla, ajustando un modelo sobre un data.frame combinado, en el que añadimos tantas filas como predicciones queremos conseguir, con los valores deseados para los predictores (y valores faltantes en la respuesta), y especificamos los valores a predecir en un vector indicador, a través del argumento control.predictor(list(link=vector.indicador)). Las predicciones se obtienen después, con el resumen de los datos ajustados fitted.values. Recordemos que para poder mostrar las distribuciones predictivas, hemos de añadir en inla el argumento control.compute=list(return.marginals.predictor=TRUE).

# Predicción con INLA
## valores de los predictores en los que predecir: 3 escenarios
formula=SO2 ~ negtemp+manuf+pop+wind+precip
new.data <- data.frame(negtemp = c(-50, -60, -40), 
                       manuf = c(150, 100, 400), 
                       pop = c(200, 100, 300), 
                       wind = c(6, 7, 8), 
                       precip = c(10, 30, 20),
                       days=c(NA, NA,NA))

## añadimos los tres escenarios de predicción a la bd original, 
## dejando como faltantes los valores a predecir de la v.dpte
usair.combinado <- rbind(usair, data.frame(SO2=c(NA,NA,NA),new.data))
## creamos un vector con NA's para observaciones y 1's para predicciones
usair.indicador <- c(rep(NA, nrow(usair)), rep(1, nrow(new.data)))
## reajustamos el modelo añadiendo la opción de predicción de datos
fit.pred <- inla(formula, data = usair.combinado, 
                 control.compute=list(return.marginals.predictor=TRUE),
                 control.predictor = list(link = usair.indicador))
## y describimos los valores ajustados para los tres escenarios añadidos
fit.pred$summary.fitted.values[(nrow(usair)+1):nrow(usair.combinado),]
#>                         mean       sd 0.025quant 0.5quant
#> fitted.Predictor.42 31.62380 8.203890   15.44856 31.62455
#> fitted.Predictor.43 26.42291 5.473735   15.63094 26.42327
#> fitted.Predictor.44 53.16293 7.091250   39.18167 53.16348
#>                     0.975quant mode
#> fitted.Predictor.42   47.79447   NA
#> fitted.Predictor.43   37.21264   NA
#> fitted.Predictor.44   67.14085   NA

Así graficamos en la Figura 2.3 la distribución predictiva del nivel de SO2 para una combinación dada de valores de las variables predictivas, específicamente la que aparece en el escenario 1 propuesto, o lo que es lo mismo, en el registro 42 de la base de datos completada con las nuevas predicciones: negtem=-50, manuf=150, pop=200, wind=6 y precip=10.

pred=fit.pred$marginals.fitted.values[[42]]
ggplot(as.data.frame(pred)) + 
  geom_line(aes(x = x, y = y)) +
  labs(x=expression(eta),y="")+
  geom_vline(xintercept=inla.hpdmarginal(0.95,pred),
             linetype="dashed",color="red")+
  geom_vline(xintercept=inla.emarginal(function(x) x,pred),
             linetype="dashed",color="blue")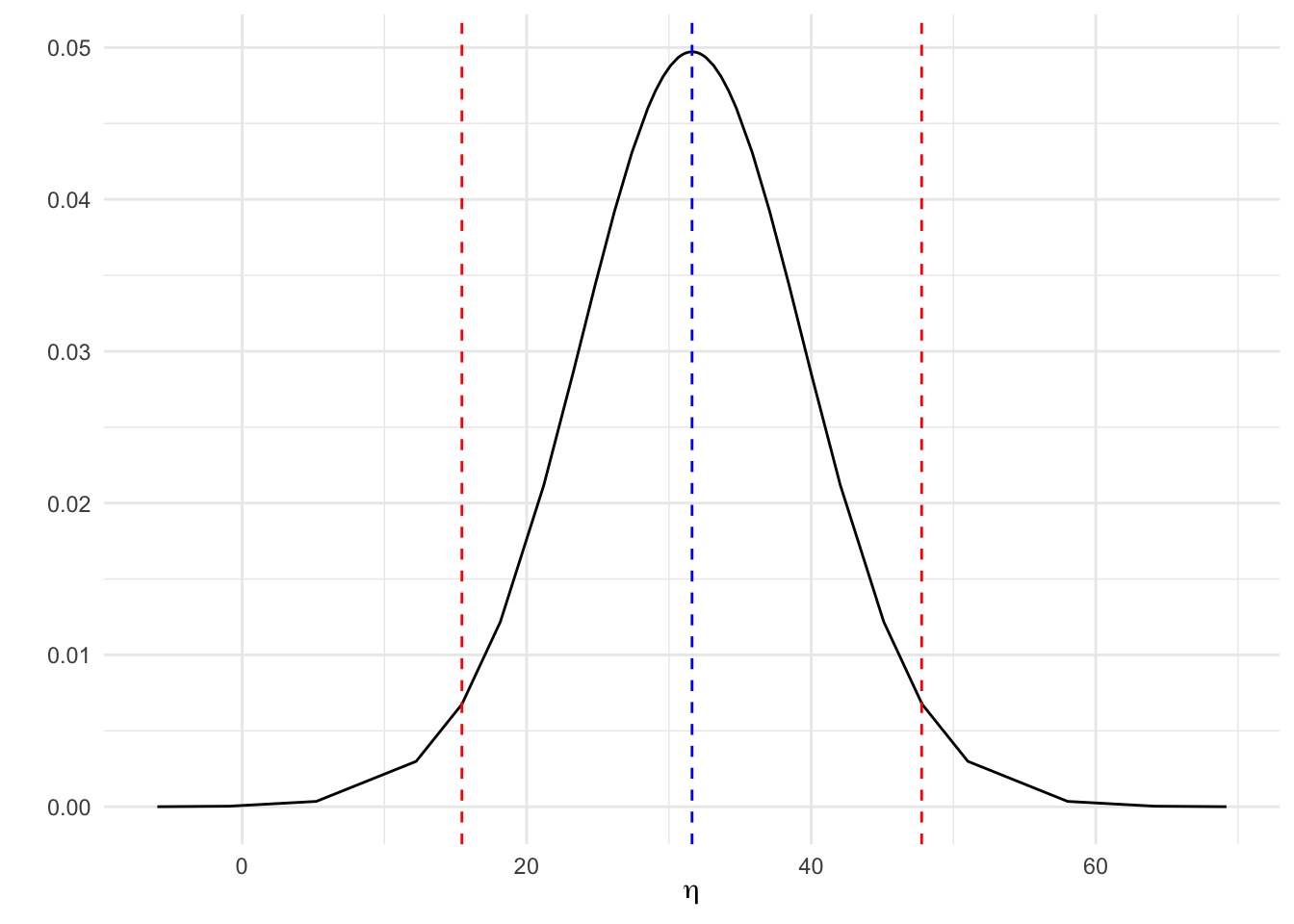

Figura 2.3: Distribución predictiva a posteriori de SO2 para una configuración dada de los predictores.

2.10 Conclusiones

En este tema hemos trabajado con el ajuste con INLA de modelos lineales de regresión, esto es, con efectos fijos. En posteriores temas trabajaremos modelos más sofisticados en los que incluiremos los efectos aleatorios, generalizaremos el modelo lineal y entenderemos el planteamiento de modelos a través de modelos jerárquicos bayesianos.

1 Contexto

3 Modelo de ANOVA