Unidad 4 Modelos lineales generalizados

Los modelos lineales generalizados, conocidos en inglés como Generalized Linear Models o GLM, son una clase de modelos introducidos por Nelder y Wedderburn (1972) y McCullagh y Nelder (1989), con el objetivo de extender la regresión lineal al caso en el que la variable dependiente no se distribuye necesariamente según una normal, pero su distribución todavía pertenece a la familia exponencial. Estamos hablando de distribuciones como la Binomial, Poisson, Gamma, o Gausiana inversa, básicamente. Trabajamos a continuación con dos de los GLM más comunes en epidemiología y ciencias sociales: la regresión logística y la de Poisson, mostrando cómo resolver este tipo de problemas con INLA.

Un modelo lineal generalizado está basado en asumir, además de una distribución de los datos dentro de la familia exponencial, una relación lineal entre cierta transformación del valor esperado de la respuesta y los predictores disponibles, sean covariables, efectos fijos, efectos aleatorios, o incluso alguna función de estos.

Si $y$ representa una respuesta observada, $x_1,x_2,..$ una serie de covariables o efectos fijos, y $z_1,z_2,...$ efectos aleatorios, y el valor esperado de la respuesta lo denotamos como $\mu$, \[E(y|x,z,\theta)=\mu\] la relación entre esta media $\mu$ y un predictor lineal $\eta$ que construimos a partir de una combinación lineal de los predictores disponibles, viene dado por una función link $g$ tal que:

\[g(\mu)=\eta=X\beta + Z u\]

Todos los parámetros involucrados en el predictor lineal $\eta$ son los efectos latentes del modelo (fijos o aleatorios). Estos, junto con el resto de parámetros definidos en este primer nivel de la modelización (nivel de datos), han de modelizarse a continuación, en un segundo nivel del modelo, con sus correspondientes distribuciones a priori.

Los modelos lineales que hemos visto antes (regresión, anova, ancova, modelos mixtos) se engloban dentro del modelo lineal generalizado.

El argumento control.predictor=list(compute=TRUE) en la función inla permite obtener las distribuciones predictivas para el predictor lineal, que en estos modelos será distinto al valor medio ajustado fitted. Además para obtener la distribución marginal de los valores ajustados y predichos necesitamos incorporar a la función inla el argumento control.compute=list(return.marginals.predictor=TRUE). Ya con todo ello podremos resumir las inferencias posteriores sobre los predictores lineales con el comando fit$summary.linear.predictor y obtener para graficar sus distribuciones posteriores con fit$marginals.linear.predictor.

4.1 Modelos jerárquicos bayesianos

A lo largo del curso ya hemos ido comentando algo sobre la especificación de un modelo en varios niveles. Presentamos ya de lleno estos modelos lineales generalizados como modelos multi-nivel o modelos jerárquicos, denominados así porque se va especificando por niveles (o jerarquías) la información disponible sobre todo aquello que es desconocido, distribución de los datos y parámetros.

Un modelo bayesiano se modeliza a través de un modelo jerárquico o multinivel en el que en el nivel I se define la distribución asumida sobre la variable respuesta y que determina la verosimilitud. Esta variable depende de unos parámetros que definen los efectos fijos y aleatorios, y para los que hay que proporcionar la información previa disponible a través de una distribución a priori en el segundo nivel del modelo jerárquico. La distribución a priori para los efectos fijos generalmente será común a todos ellos, mientras que la distribución a priori para los efectos aleatorios estará vinculada a otros hiperparámetros para los que también será preciso especificar una distribución a priori en un tercer nivel de la modelización, y así sucesivamente. Podríamos esquematizar un modelo jerárquico, a grosso modo, a través de la siguiente jerarquía.

\[\begin{eqnarray*} Nivel I &&\\ ( y | \beta,u,\Sigma) &\sim & f(y|\beta,u,\Sigma) \\ && E(y|\beta,u,\Sigma)=\mu; Var(y|\beta,u,\Sigma)=\Sigma \\ && g(\mu)=\eta=X\beta + Z u \\ Nivel II &&\\ \beta &\sim & N(0,\sigma_{\beta}^2), \ \ \sigma_{\beta}^2 \text{ fijo} \\ (u|\sigma_u^2) &\sim_{iid}& N(0,{\sigma_u^2}) \\ \Sigma|\sigma &\sim& F_{\Sigma|\sigma} \\ Nivel III &&\\ \sigma_u^2 &\sim& F_{\sigma_u} \\ \sigma &\sim& F_{\sigma} \end{eqnarray*}\]

4.2 Regresión logística

La regresión logística es el modelo estándar para respuestas binarias (éxitos/fracasos). Tiene dos variaciones, en función de si la respuesta viene dada en función de las observaciones individuales (0/1), o de los conteos (número de éxitos en $n$ pruebas).

Si las observaciones de éxitos-fracasos vienen individualizadas, tenemos que la respuesta es directamente modelizable con una distribución Bernouilli:

\[Y|\pi \sim Ber(\pi) \rightarrow E(Y)=\pi\] En el caso de que los datos vengan agrupados a modo de conteos de éxitos en diversos grupos poblacionales, modelizaremos con distribuciones Binomiales de tamaño $n$, que podría variar en cada grupo:

\[(Z=\sum_{i=1}^n Y_i)|\pi\sim Bin(n,\pi)\rightarrow E(Z)=n\pi\] En cualquiera de los casos, el objetivo es inferir sobre la probabilidad de éxito $\pi$. El modelo logit utiliza la función logit para relacionar el predictor lineal $\eta$ y la probabilidad $\pi$: \[logit(\pi)=log\left(\frac{\pi}{1-\pi}\right)=\eta=X\beta+Zu\] de forma que \[\pi=logit^{-1}(X\beta+Zu)=\frac{exp(X\beta+Zu)}{1-exp(X\beta+Zu)}\] Una vez especificado el modelo, si no hay información previa disponible sobre los efectos latentes $(\beta,u)$, se asumen las distribuciones a priori habituales, generalmente normales independientes con media cero y varianza grande para efectos fijos y varianza desconocida para efectos aleatorios. En un tercer nivel se habrá de modelizar la información a priori de las varianzas para los efectos aleatorios.

4.2.1 Interpretación de los coeficientes en la regresión logit

Por simplificar la interpretación de los coeficientes, vamos a asumir que la respuesta es Bernouilli y todos los efectos latentes son fijos, de modo que el predictor lineal se puede escribir como: \[\eta=X\beta=\beta_0+\sum_{j=1}^M \beta_j x_{j}\]

A partir de esta expresión se entiende claramente que la interceptación del predictor lineal $\beta_0$ se interpreta como el valor del predictor cuando las variables predictivas toman el valor cero si son numéricas, o cuando se refieren al nivel de referencia si son categóricas, es decir,
\[\beta_0=\eta_{(X=0)}=logit(\pi_{(X=0)})\]

En consecuencia, el logit inverso de $\beta_0$ se interpreta como “la probabilidad de éxito cuando los predictores están en su nivel de referencia o son cero”.

\[logit^{-1}(\beta_0)=\pi_{(X=0)}=Pr(Y=1|X=0)\]

En cuanto a la interpretación de cualquier otro coeficiente de regresión en el predictor lineal, como $\beta_1$, echamos mano del concepto de odds y odds ratio.

Los odds de un evento $E$ se definen a través de las posibilidades de que se dé dicho evento, y se calcula con el cociente de su probabilidad y la probabilidad de que no se dé: \[odds(E)=\frac{Pr(E)}{1-Pr(E)}\]

Los odds ratio, OR de un evento relativo a dos condiciones A y B, comparan, a través de un cociente, las posibilidades a favor del evento $E$ bajo condiciones A y sus posibilidades bajo condiciones B. Nos sirve para evaluar cuánto afectan a las posibilidades del evento el hecho de variar las condiciones de B a A. \[OR(A,B)=\frac{Pr(E|A)/(1-Pr(E|A))}{Pr(E|B)/(1-Pr(E|B))}.\]

En el modelo logístico, nos interesa saber el efecto que tiene sobre la respuesta (realmente sobre la probabilidad de éxito) el incremento de una unidad en la variable predictora $X$, y para ello consideramos los odds bajo $X=x$ y los odds bajo $X=x+1$, esto es, las posibilidades de éxito bajo $x$ y bajo $x+1$. Si además consideramos estos odds en escala logarítmica, esto es, los log-odds, tenemos:

\[\begin{eqnarray*} log.odds(x+1)&=&log \left( \frac{P(y=1|x+1)}{P(y=0|x+1)} \right)\\ &=&logit(\pi_{(x+1)}) =\beta_0+\beta_1 (x+1) \\ log.odds(x) &=& log \left(\frac{P(y=1|x)}{P(y=0|x)} \right)\\ &=&logit(\pi_{(x)})=\beta_0+\beta_1 x \end{eqnarray*}\]

Así tendremos que el logaritmo del odds-ratio coincide con el coeficiente que relaciona $X$ con el predictor lineal, esto es, $\beta_1$:
\[\begin{eqnarray*} log(OR(x+1,x)) &=& log \left(\frac{ods (x+1)}{ods(x)} \right) \\ &=& log.odds(x+1)-log.ods(x)= \beta_1 \end{eqnarray*}\]

Es decir, la exponencial del coeficiente $\beta_1$ nos da el odds ratio asociado a dicha covariable, esto es, el cambio en los odds a favor de un éxito cuando se incrementa en una unidad la variable predictora $X$. Esta interpretación es muy común en Epidemiología.

\[exp(\beta_1)=\frac{odds(x+1)}{odds(x)}=OR(x+1,x).\] Cuando estamos ante un predictor categórico, la exponencial del coeficiente estimado para un nivel o categoría $i$ representa la variación en los odds que se produce al pasar del nivel base del factor al nivel $i$. Si dicha variación es superior a 1, entonces hablamos de que es más probable el evento, y si es inferior a 1, decimos que es menos probable cuando estamos en el nivel $i$ que en el nivel 1.

4.2.2 Intención de voto feb2022

Tenemos acceso a los datos completos obtenidos en la encuesta encargada por El País y la Cadena Ser a la empresa “40dB”, en febrero de 2022, sobre la intención de voto nacional en España (fuente).

Queremos predecir la probabilidad de votar al partido que gobierna mayoritariamente en la actualidad, PSOE, registrado en la variable psoe. Vamos a utilizar como predictores dos factores que nos dicen si el sujeto tiene simpatía por ese partido, psoe_sim, y si votó PSOE en las últimas elecciones psoe_past; también utilizaremos la comunidad autónoma ccaa como un efecto aleatorio, para contabilizar posible variación extra (igualmente podríamos considerarla como un efecto fijo).

url="https://raw.githubusercontent.com/BayesModel/data/main/barometro_feb22.csv"
barometro_feb22=read.csv(url)
datos=barometro_feb22 %>%
  select(id,p2,p3,p5,ccaa) %>%
  mutate(psoe=1*(p2=="PSOE (Partido Socialista Obrero Español)"),
         psoe_simp=1*(p3=="PSOE (Partido Socialista Obrero Español)"),
         psoe_past=1*(p5=="PSOE (Partido Socialista Obrero Español)")) 
#summary(datos)

Especificamos pues un modelo que asume para los efectos fijos las distribuciones difusas por defecto en INLA, y para la varianza de los efectos aleatorios una $GaI(0.001,0.001)$.

\[\begin{eqnarray*} y_{ijkl}|\pi_{ijk} & \sim & Br(\pi_{ijk}) \\ logit(\pi_{ijk}) =\eta_{ijk} &=& \theta + \alpha_i^{simp} + \alpha_j^{past} + \gamma_{k}^{ca} \\ \theta &\sim& N(0,\infty) \\ \alpha_i^{simp}&\sim& N(0,1000), i=2\\ \alpha_j^{past}&\sim& N(0,1000), j=2 \\ \gamma_k^{ca} &\sim& N(0,\sigma_{ca}^2) , k=2,...,17\\ 1/\sigma_{ca}^2 &\sim& Ga(0.001,0.001) \end{eqnarray*}\]

Las inferencias posteriores se resumen en los siguientes descriptivos.

prec.prior=list(prec=list(param=c(0.001,0.001)))
formula = psoe ~ psoe_simp + psoe_past+ f(ccaa,model="iid",hyper=prec.prior)
fit=inla(formula,family="binomial",data=datos)
round(fit$summary.fixed[,1:5],3)
#>               mean    sd 0.025quant 0.5quant 0.975quant
#> (Intercept) -3.591 0.190     -3.999   -3.578     -3.251
#> psoe_simp    3.086 0.187      2.724    3.084      3.456
#> psoe_past    2.352 0.186      1.990    2.352      2.718
round(fit$summary.hyperpar[,1:5],3)
#>                      mean      sd 0.025quant 0.5quant
#> Precision for ccaa 70.843 250.892      1.978   10.689
#>                    0.975quant
#> Precision for ccaa    589.342
head(round(fit$summary.fitted.values[,1:5],3))
#>                        mean    sd 0.025quant 0.5quant
#> fitted.Predictor.0001 0.026 0.007      0.014    0.026
#> fitted.Predictor.0002 0.033 0.007      0.022    0.032
#> fitted.Predictor.0003 0.029 0.006      0.019    0.029
#> fitted.Predictor.0004 0.029 0.006      0.019    0.029
#> fitted.Predictor.0005 0.033 0.007      0.022    0.032
#> fitted.Predictor.0006 0.882 0.023      0.835    0.883
#>                       0.975quant
#> fitted.Predictor.0001      0.040
#> fitted.Predictor.0002      0.049
#> fitted.Predictor.0003      0.042
#> fitted.Predictor.0004      0.042
#> fitted.Predictor.0005      0.049
#> fitted.Predictor.0006      0.926
head(round(fit$summary.linear.predictor[,1:5],3))
#>                  mean    sd 0.025quant 0.5quant 0.975quant
#> Predictor.0001 -3.651 0.269     -4.242   -3.626     -3.181
#> Predictor.0002 -3.394 0.209     -3.798   -3.398     -2.973
#> Predictor.0003 -3.524 0.207     -3.951   -3.517     -3.131
#> Predictor.0004 -3.524 0.207     -3.951   -3.517     -3.131
#> Predictor.0005 -3.394 0.209     -3.798   -3.398     -2.973
#> Predictor.0006  2.035 0.232      1.623    2.018      2.527

La variabilidad para los efectos aleatorios es relevante, como se manifiesta a través de la distribución posterior de su varianza, que se muestra en la Figura 4.1 en términos de $\sigma_{ca}$.

sigma.post=inla.tmarginal(function(tau) tau^(-1/2),
  fit$marginals.hyperpar[[1]])
# y la pintamos
ggplot(as.data.frame(sigma.post)) + 
  geom_line(aes(x = x, y = y)) +
  labs(x=expression(sigma),y="D.Posterior")+
  geom_vline(xintercept=inla.hpdmarginal(0.95,sigma.post),
             linetype="dotted",color="blue")+
  geom_vline(xintercept=inla.emarginal(function(x) x,sigma.post),
             linetype="dashed",color="blue")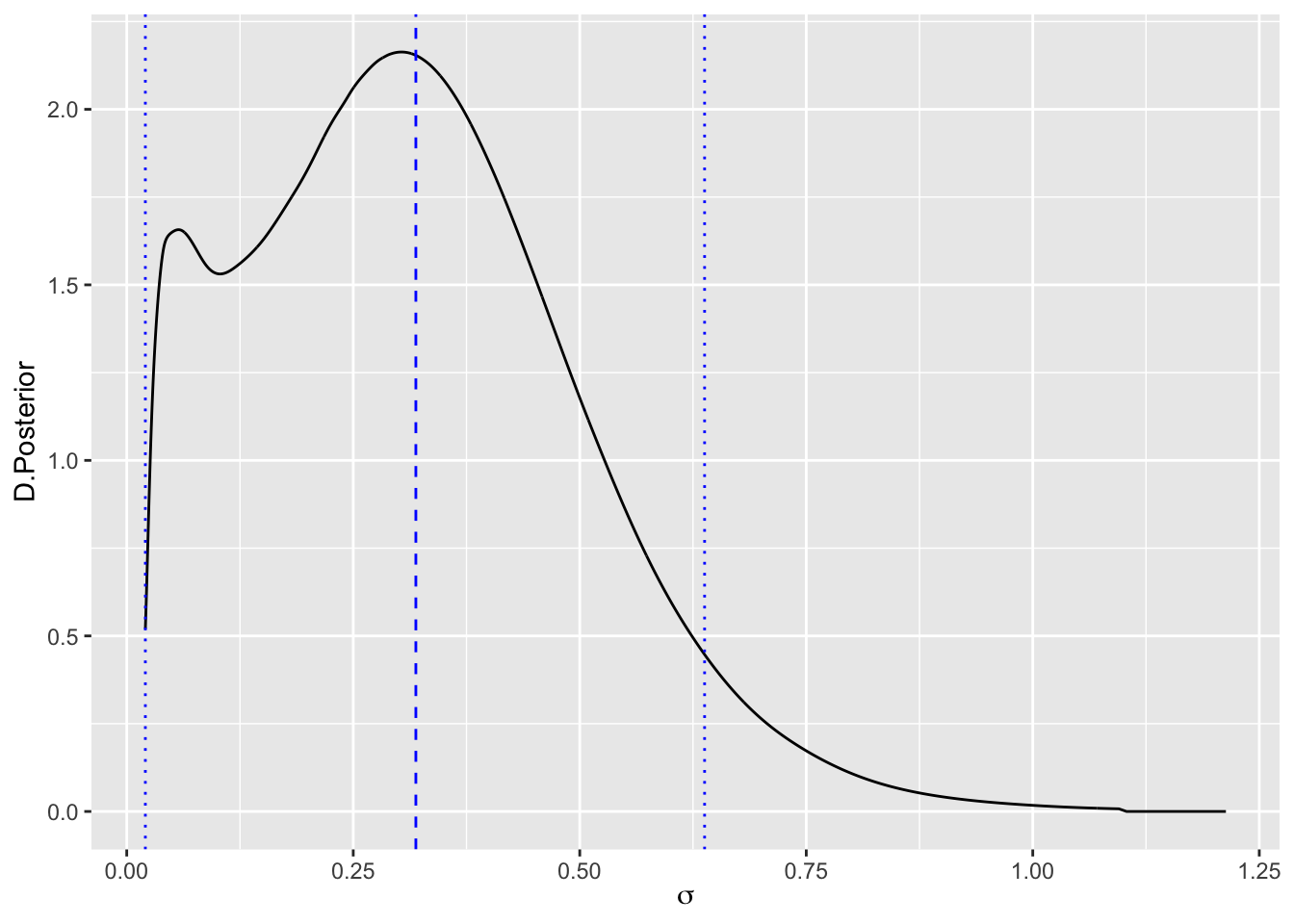

Figura 4.1: Distribución posterior, media y RC, de la desviación típica de los efectos aleatorios


# Valor esperado
sigma.e=round(inla.emarginal(function(tau) tau^(-1/2),
  fit$marginals.hyperpar[[1]]),4)
# HPD95%
sigma.hpd=round(inla.hpdmarginal(0.95,sigma.post),3)
paste("E(sigma.post)=",sigma.e,
      "HPD95%=(",sigma.hpd[1],",",sigma.hpd[2],")")
#> [1] "E(sigma.post)= 0.3189 HPD95%=( 0.021 , 0.638 )"

Las distribuciones posteriores de los exponenciales de los efectos aleatorios (que representan los odds-ratios) se muestran en la Figura 4.2, en términos de medias y regiones creíbles. Están identificadas en verde las comunidades con efectos positivos hacia el voto PSOE (odds>1), y en rojo las de efectos negativos (odds<1). Estas distribuciones de efectos aleatorios nos permiten diferenciar qué comunidades autónomas son más (verde) y menos (rojo) favorables a votar por el PSOE, en términos de valor esperado (a posterior), así como descubrir la incertidumbre y variabilidad existente en dichas afirmaciones, dada por la región creíble.

random = as.data.frame(fit$summary.random)
random$pro=1*exp(random$ccaa.mean)>1
ggplot(random,aes(x=exp(ccaa.mean),y=ccaa.ID)) +
  geom_point(aes(color=pro))+
  geom_errorbarh(aes(xmin=exp(ccaa.0.025quant),
          xmax=exp(ccaa.0.975quant),color=pro))+
  geom_vline(xintercept=1,linetype="dotted")+
  labs(x="Medias y RC posteriores para los odds-ratio",
       y="Comunidad autónoma")+
  theme(legend.position="none")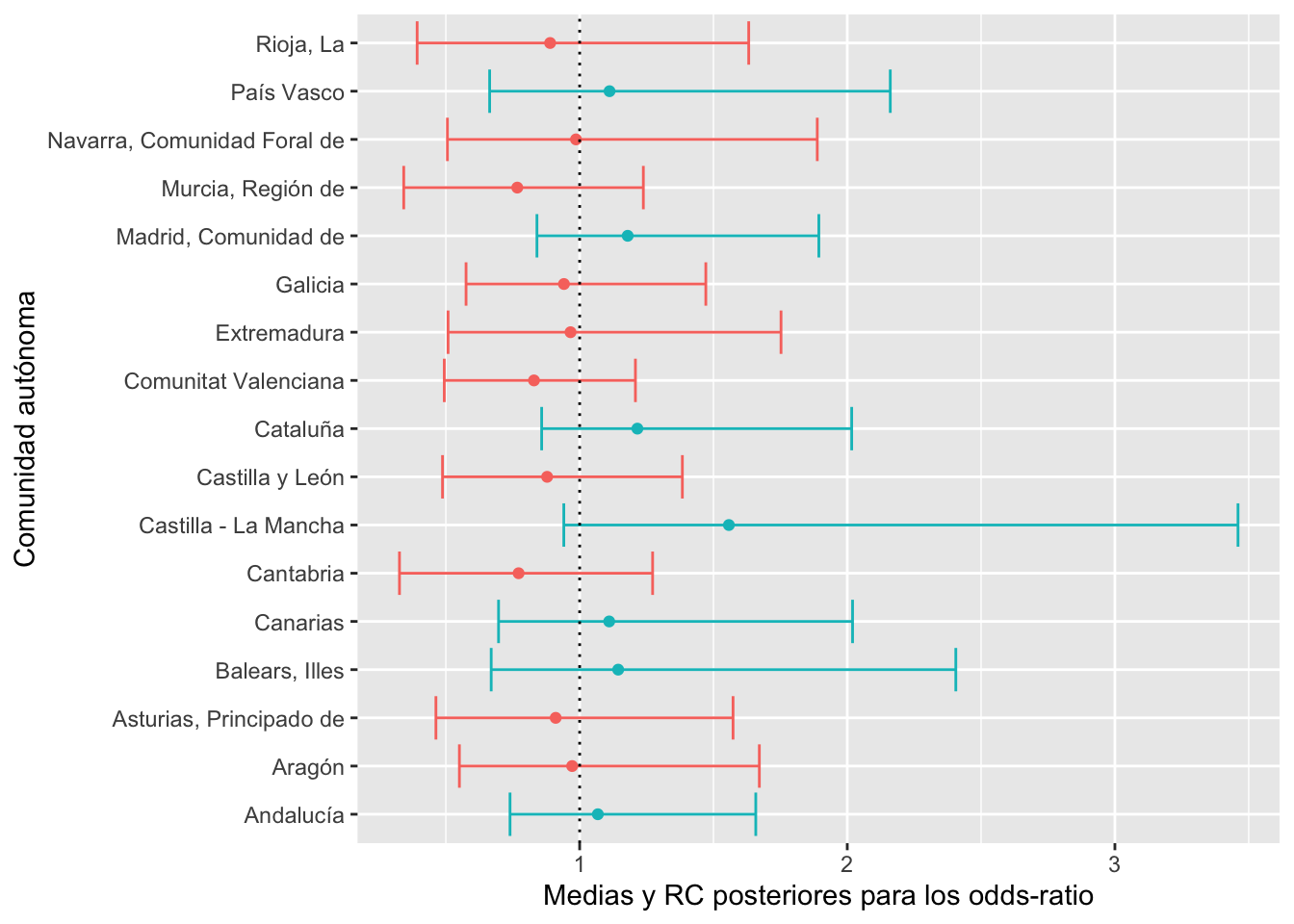

Figura 4.2: Medias y RC posteriores para los odds-ratios de los efectos aleatorios

La distribución posterior de la probabilidad de voto para el PSOE la conseguimos a través de los valores ajustados, fitted. En la Figura 4.3 está representada la inferencia posterior sobre la probabilidad de voto para cada uno de los cuatro colectivos que identificamos en función de su simpatía por el PSOE y su voto en el pasado, en la comunidad autónoma con más variabilidad en el efecto aleatorio, esto es, Castilla-La Mancha.

datos_pred = datos %>%
  mutate(f.post=round(fit$summary.fitted.values$mean,3),
    f.rc.low=round(fit$summary.fitted.values$"0.025quant",3),
    f.rc.up=round(fit$summary.fitted.values$"0.975quant",3)) %>%
  distinct(f.post,.keep_all = TRUE) %>%
  filter(ccaa=="Castilla - La Mancha") %>%
  mutate(simpast=str_c(psoe_simp,psoe_past))

ggplot(datos_pred,aes(x=f.post,y=simpast))+
  geom_point(aes(color=simpast))+
  geom_errorbarh(
    aes(xmin=f.rc.low,xmax=f.rc.up,color=simpast),
    height=0.2)+
  labs(x="Medias y RC posteriores para la probabilidad de voto PSOE",
       title="Castilla - La Mancha")+
  scale_y_discrete(name="", 
        labels=c("No simpatía/No votó PSOE","No simpatía/Votó PSOE",
           "Simpatía/No votó PSOE","Simpatía/Votó PSOE"))+
  theme(legend.position="none")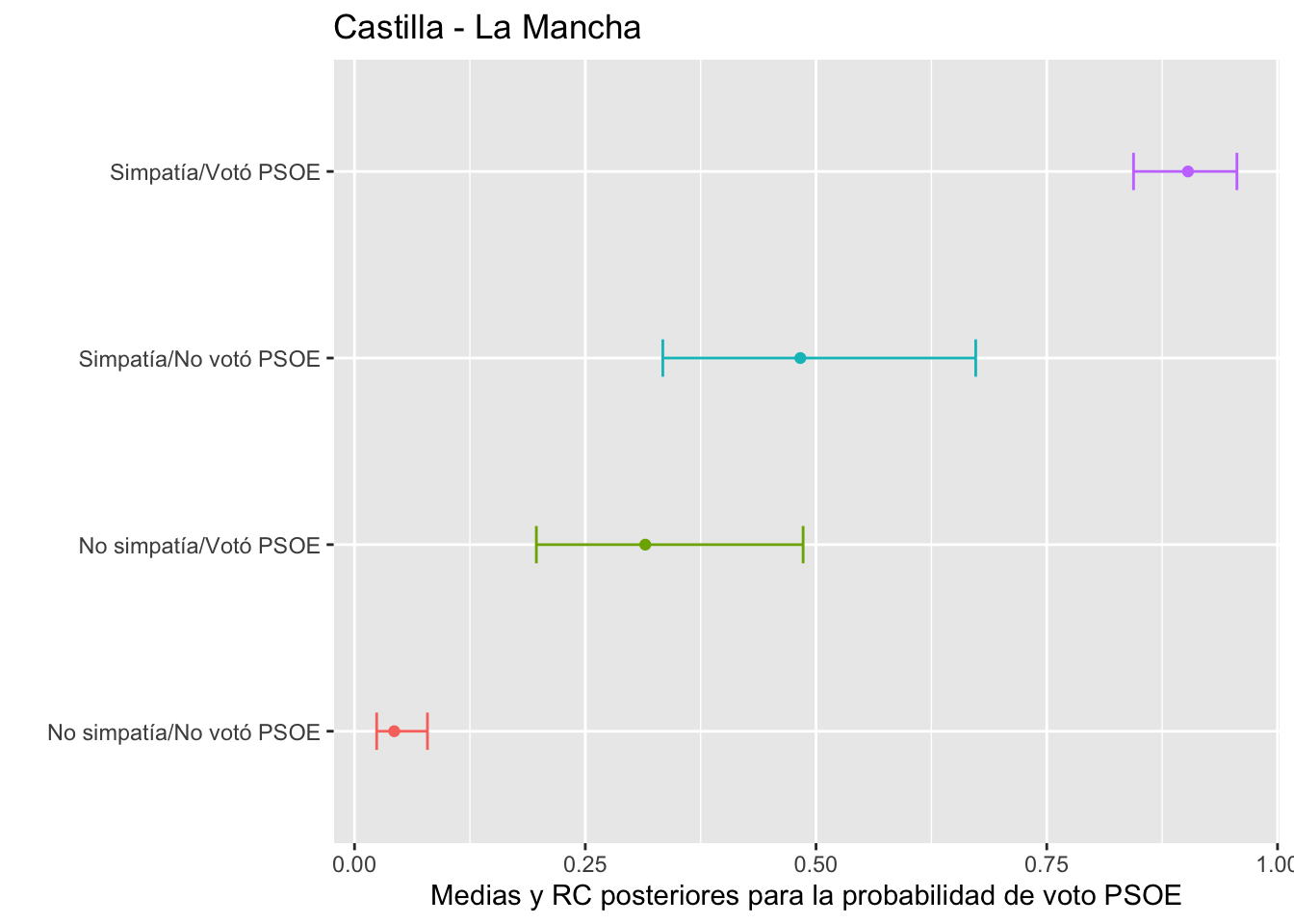

Figura 4.3: Medias y RC posteriores para la probabilidad de voto PSOE

4.2.3 Mortalidad por infarto en Sheffield

Utilizamos los datos stroke, disponibles en datasets in SSTM-RINLA relativos al periodo 1994-1999. El objetivo es evaluar la asociación entre los niveles de NOx y el infarto en Sheffield (UK). Utilizaremos la siguiente información:

número de infartos y en cada distrito,
una agrupación de distritos en base a cierto índice relativo al nivel de desventajas y privación en dicho distrito, Townsend (en escala 1-5),
la concentración anual media de NOx, categorizada en cinco niveles (escala 1-5)
el tamaño de la población en cada distrito, pop
el riesgo base ajustado por sexo y edad para el número de infartos, calculado con estandarización indirecta con ratios de referencia internos basados en 18 estratos (9 para edad y 2 para género), en la variable stroke_exp (Maheswaran et al.2006).

La respuesta $y_{ijk}$ relativa al número de infartos en el distrito $k$ en el nivel $i$ de NOx y $j$ de Townsend, con una población $n_{ijk}$, se puede modelizar con:

\[y_{ijk}|\pi_{ij} \sim Bin(n_{ijk}, \pi_{ij})\]

Planteamos las asociaciones que intuimos a través del predictor lineal, definido en función del nivel de NOx y el nivel de privación Townsend, ambos como efectos fijos, así como de offset que representa el riesgo base corregido por el tamaño del distrito, $\tilde{p_i}=$stroke_exp/pop, en escala logit.

\[\eta_{ij}=logit(\pi_{ij})=\theta + \alpha_i^{NOx} + \alpha_j^{Town} + Offset(logit(\tilde{p_i}))\] Ajustamos pues el modelo con los efectos fijos NOx y Townsend, y el offset que calculamos y llamamos logit.adjusted.prob, que proporciona una estandarización del riesgo en base al tamaño de población en cada distrito, y para el que no se estima coeficiente.

url="https://raw.githubusercontent.com/BayesModel/data/main/Stroke.csv"
Stroke <- read.csv(url,sep=",",dec=".",header=TRUE)
# conversión a factores y cálculo del riesgo base
stroke=Stroke %>%
  mutate(NOx=as.factor(NOx),Townsend=as.factor(Townsend),
         adjusted.prob=stroke_exp/pop,
         logit.adjusted.prob=log(adjusted.prob/(1-adjusted.prob)))

# ajuste del modelo
formula.inla <- y ~ 1 + NOx + Townsend + offset(logit.adjusted.prob)
fit <- inla(formula.inla, family="binomial", Ntrials=pop, data=stroke)
round(fit$summary.fixed[,1:5],3)
#>               mean    sd 0.025quant 0.5quant 0.975quant
#> (Intercept) -0.181 0.057     -0.293   -0.180     -0.071
#> NOx2         0.132 0.059      0.016    0.132      0.248
#> NOx3         0.105 0.061     -0.014    0.105      0.225
#> NOx4         0.261 0.059      0.144    0.260      0.377
#> NOx5         0.425 0.062      0.302    0.425      0.547
#> Townsend2    0.077 0.061     -0.043    0.077      0.198
#> Townsend3    0.137 0.060      0.020    0.137      0.255
#> Townsend4   -0.132 0.063     -0.255   -0.132     -0.009
#> Townsend5   -0.118 0.067     -0.250   -0.118      0.014

Inferimos sobre la probabilidad esperada de infarto en un distrito con niveles base en privación Townsend y NOx, esto es, Townsend=1 y NOx=1, con la distribución posterior del logit inverso de la interceptación $\theta$. Esta distribución posterior la obtendremos entonces a partir de simulaciones de la distribución posterior de $\theta$ y utilizando la función logit-inversa \[logit^{-1}(\theta)=\frac{exp(\theta)}{1+exp(\theta)}\]

prob.stroke <- inla.tmarginal(function(x) exp(x)/(1+exp(x)), fit$marginals.fixed[[1]])
des=inla.zmarginal(prob.stroke)
#> Mean            0.455034 
#> Stdev           0.0139168 
#> Quantile  0.025 0.427486 
#> Quantile  0.25  0.445615 
#> Quantile  0.5   0.455082 
#> Quantile  0.75  0.464485 
#> Quantile  0.975 0.482137
ggplot(data.frame(prob.stroke),aes(x=x,y=y))+
  geom_line()+
  geom_vline(xintercept=des$mean,linetype="dashed",color="red")+
  geom_vline(xintercept=c(des$"quant0.025",des$"quant0.975"),
             linetype="dotted",color="blue")+
  labs(x=expression(pi),
       y= expression(paste("DPosterior|",NOx[1],",",TS[1])))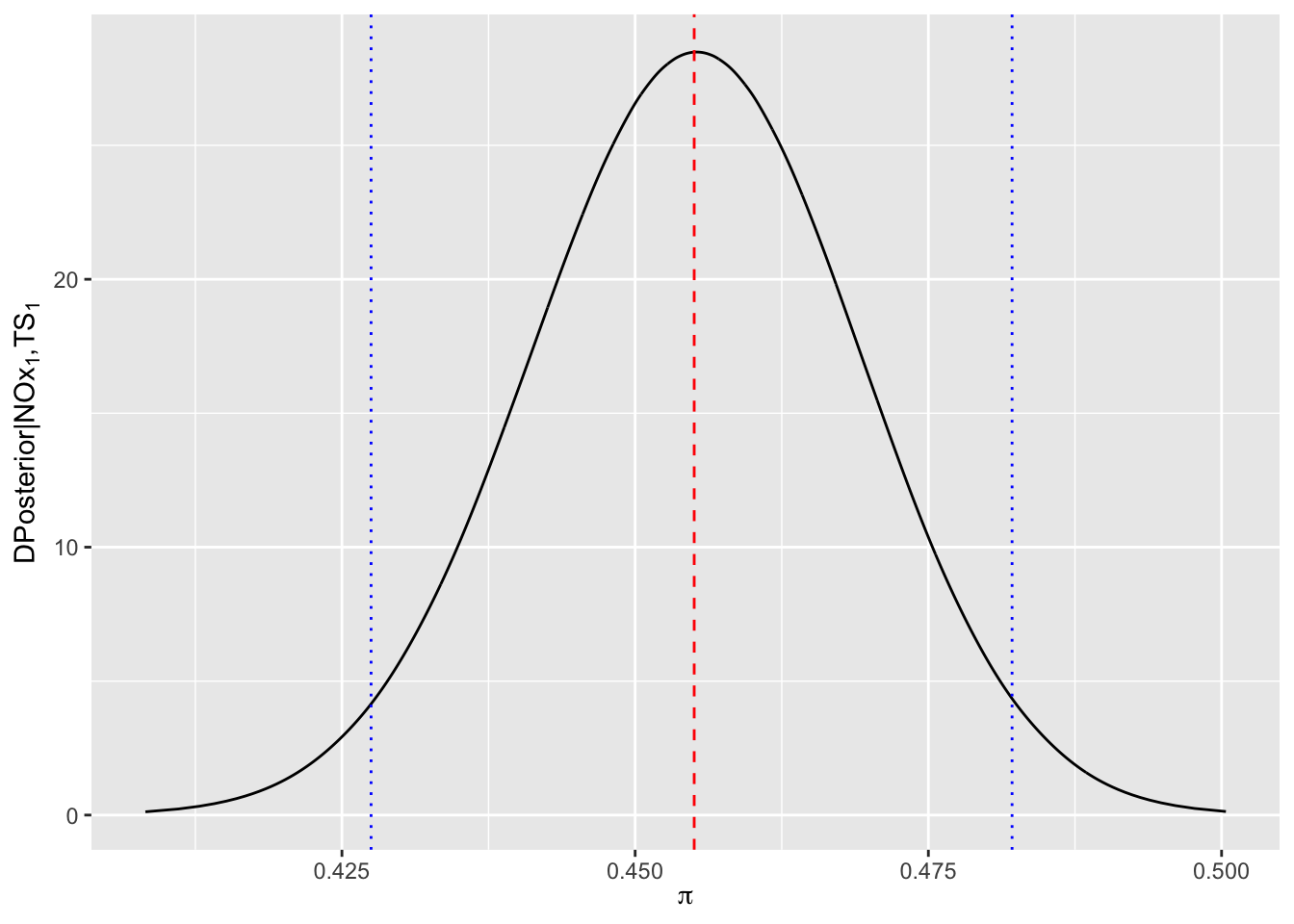

El efecto $\alpha_2^{NOx}$ representa el efecto diferencial en los log-odds del infarto al estar en el nivel $NOx=2$ frente al de estar en el nivel de referencia $NOx=1$. Si queremos evaluar el odds-ratio, simplemente calculamos la distribución posterior de $exp(\alpha_2^{NOx})$ con inla.tmarginal. Si sólo estamos interesados en sus descriptivos posteriores bastaría utilizar inla.zmarginal.

odds.nox21 <- inla.tmarginal(exp, 
                             fit$marginals.fixed$NOx2)
m=inla.emarginal(exp,fit$marginals.fixed$NOx2)
hpd=inla.hpdmarginal(0.95,odds.nox21)
ggplot(data.frame(odds.nox21),aes(x=x,y=y))+
  geom_line()+
        labs(x=expression(OR(NOx[21])),
             y= "DPosterior")+
geom_vline(xintercept=m,linetype="dashed",color="red")+
  geom_vline(xintercept=hpd,
             linetype="dotted",color="blue")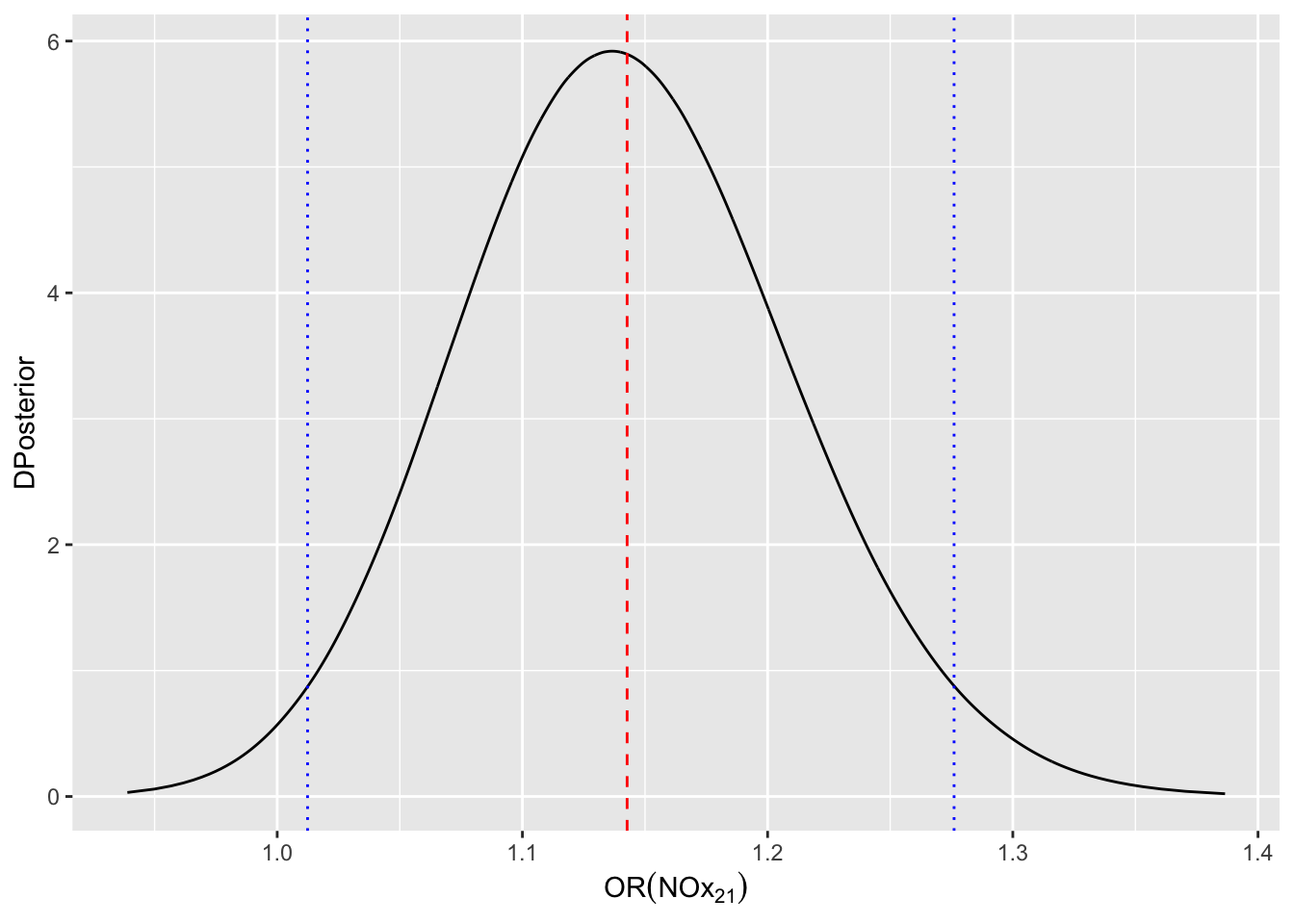

Concluimos pues, que la probabilidad de muerte por infarto se incrementa en un -54.5 cuando la exposición de NOx cambia del primer al segundo nivel (la región creíble da un margen de crecimiento entre -57.25 y -51.79.

Los odds-ratio para el resto de los niveles resultan igualmente “significativos” desde el punto de vista bayesiano, teniendo en cuenta sus estimaciones (media de la distribución posterior) e intervalos creíbles:

OR31=inla.zmarginal(inla.tmarginal(function(x) exp(x), 
                             fit$marginals.fixed$NOx3))
#> Mean            1.1131 
#> Stdev           0.0673074 
#> Quantile  0.025 0.986696 
#> Quantile  0.25  1.06638 
#> Quantile  0.5   1.11095 
#> Quantile  0.75  1.1574 
#> Quantile  0.975 1.25097
OR41=inla.zmarginal(inla.tmarginal(function(x) exp(x), 
                             fit$marginals.fixed$NOx4))
#> Mean            1.29988 
#> Stdev           0.0766197 
#> Quantile  0.025 1.15596 
#> Quantile  0.25  1.24669 
#> Quantile  0.5   1.29744 
#> Quantile  0.75  1.35031 
#> Quantile  0.975 1.4568
OR51=inla.zmarginal(inla.tmarginal(function(x) exp(x), 
                             fit$marginals.fixed$NOx5))
#> Mean            1.53223 
#> Stdev           0.0950874 
#> Quantile  0.025 1.35392 
#> Quantile  0.25  1.46617 
#> Quantile  0.5   1.52909 
#> Quantile  0.75  1.59475 
#> Quantile  0.975 1.72726

rbind(OR31,OR41,OR51)[,c(1,2,3,7)]
#>      mean     sd         quant0.025 quant0.975
#> OR31 1.113102 0.06730743 0.9866958  1.250967  
#> OR41 1.29988  0.07661972 1.155961   1.456801  
#> OR51 1.532227 0.09508741 1.353922   1.727261

4.3 Regresión de Poisson

La regresión de Poisson es útil cuando la variable respuesta representa conteos y estos toman valores discretos entre 0 y $+\infty$, sin una cota superior de referencia. El parámetro de interés es el número promedio de eventos $\lambda=E(y)$ y el link natural es el logaritmo, de modo que el predictor lineal está ligado con las covariables y factores según:

\[\begin{eqnarray*} y &\sim& Po(\lambda) \\ \eta=log(\lambda)=X \beta+Zu, && \lambda=exp(X \beta+Zu) \end{eqnarray*}\]

Para completar el modelo bayesiano, se especifican distribuciones a priori para los coeficientes de los efectos fijos y aleatorios, $(\beta,u)$, típicamente como normales con media cero y una varianza grande para efectos fijos $\beta$ cuando no hay información previa disponible, y varianzas desconocidas para los efectos aleatorios $u$. En el siguiente nivel se especificarán gammas dispersas para la precisión de los efectos aleatorios.

Los coeficientes se interpretan a través de la función exponencial. Supongamos por simplicidad, un predictor lineal de la forma $\eta=\theta+\sum_{i=1}^M \beta_i x_i$:

$exp(\theta)$ representa el valor esperado de la respuesta cuando todas las covariables son cero, o si son categóricas para el primer nivel de las categorías posibles.
$exp(\beta_i)$ es el cambio que se produce en la respuesta promedio $y$ cuando $x_i$ se incrementa en una unidad si dicha variable es numérica, o el cambio que se produce al pasar del primer nivel o categoría al nivel $i$.

La mayoría de las veces que se utiliza la regresión de Poisson, el interés recae en las ratios o riesgos relativos, más que en el número esperado de casos $\lambda$. Para cambiar la escala en términos de riesgo $\rho$, generalmente expresado con $\lambda=\rho \cdot E$, ha de utilizarse un offset $E$ como factor de corrección en la especificación del modelo. Este offset representa el denominador común del riesgo, o riesgo base, y entra en la regresión en una escala logarítmica (dada la función link), asumiendo que tiene un coeficiente de regresión fijado a 1, es decir, no se estima coeficiente para él.

\[\eta=log(\lambda)=X\beta+Zu+log(E)\]

Así, el riesgo relativo de que se produzca un evento se calculará dividiendo por el riesgo base, que en escala logarítmica será \[log\left(\frac{\lambda}{Offset}\right)\]

y al exponenciar los coeficientes $exp(\beta)$, podremos interpretarlos como el cambio que se produce en el riesgo relativo al incrementar en una unidad el predictor correspondiente, si es continuo, o al pasar del nivel base al nivel que representa dicho coeficiente.

4.3.1 Roturas de hilo

La base de datos warpbreaks en la librería datasets proporciona el número de roturas breaks en el hilado en cada telar, para una serie de telares de longitud común. Contiene también información sobre el tipo de lana (A y B), wool y el nivel de tensión del telar (L,M,H), tension. En la Figura 4.4 se representan los datos.

data(warpbreaks, package="datasets")
ggplot(warpbreaks,aes(x=tension,y=breaks))+
  geom_boxplot(aes(color=wool))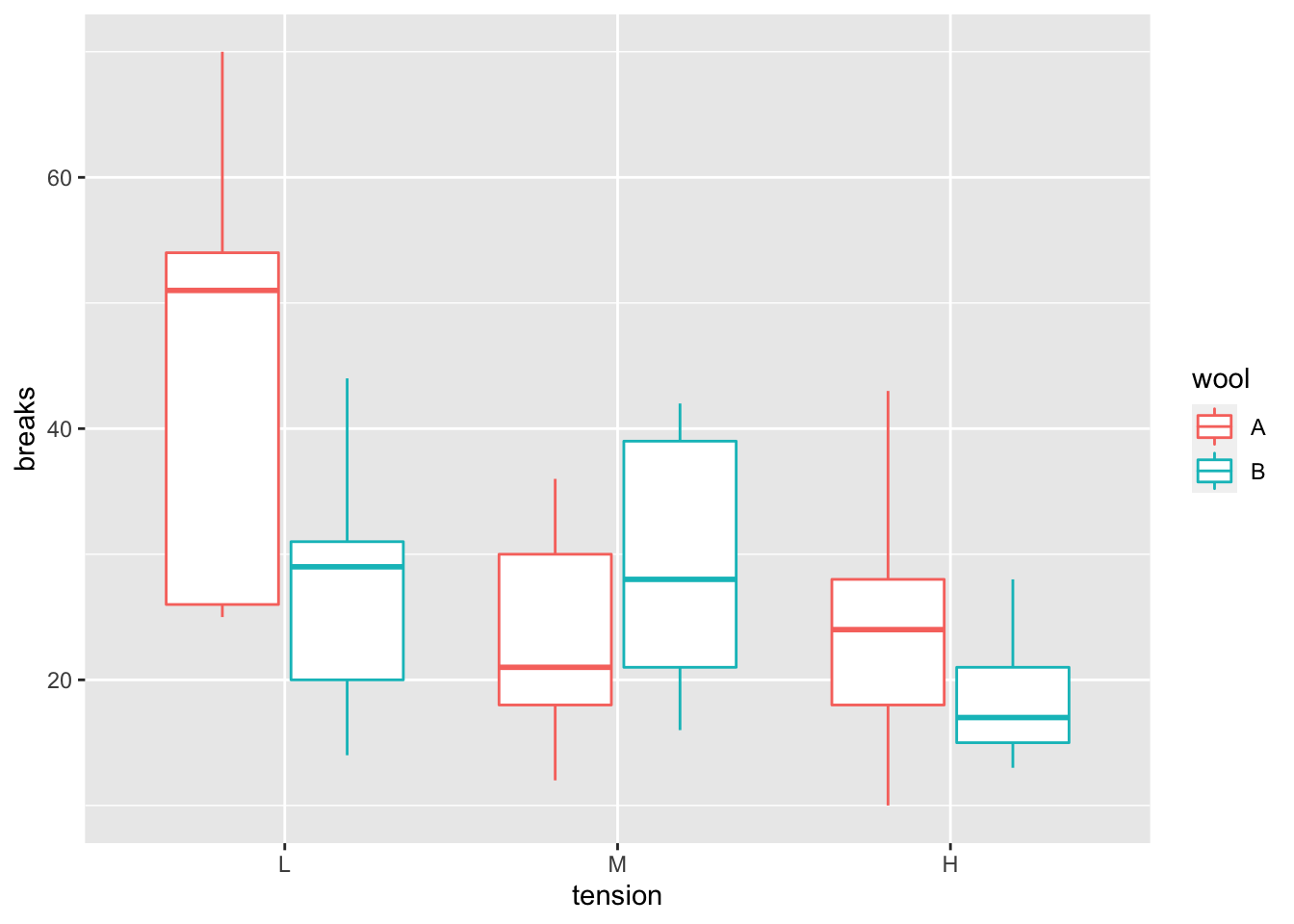

Figura 4.4: Relaciones en la base de datos warpbreaks

Queremos pues predecir el número de roturas en un telar $k$, en función del tipo de lana $i$ y la tensión del telar $j$, que consideramos como efectos fijos.

\[ y_{ijk}|\lambda_{ij} \sim Po(\lambda_{ij}) \\ log(\lambda_{ij})=\eta_{ij}=\theta+ \alpha_i^w+ \alpha_j^t\]

Ajustamos el modelo anterior con las priors por defecto y obtenemos:

formula= breaks ~ wool + tension
fit=inla(formula,family="poisson",data=warpbreaks,
         control.compute=list(return.marginals.predictor=TRUE))
round(fit$summary.fixed[,1:5],3)
#>               mean    sd 0.025quant 0.5quant 0.975quant
#> (Intercept)  3.692 0.045      3.602    3.692      3.780
#> woolB       -0.206 0.052     -0.307   -0.206     -0.105
#> tensionM    -0.321 0.060     -0.440   -0.321     -0.203
#> tensionH    -0.518 0.064     -0.645   -0.518     -0.393

Los efectos fijos expresados con sus distribuciones posteriores completas los representamos en la Figura 4.5.

fixed=names(fit$marginals.fixed)
g=list()
for(i in 1:length(fixed)){
  g[[i]]=ggplot(as.data.frame(fit$marginals.fixed[[i]]),aes(x=x,y=y))+
    geom_line()+
    geom_vline(xintercept=fit$summary.fixed$mean[i],linetype="dashed")+
    geom_vline(xintercept=fit$summary.fixed[i,3],linetype="dotted")+
    geom_vline(xintercept=fit$summary.fixed[i,5],linetype="dotted")+
    labs(x=fixed[i],y="D.posterior")
}
grid.arrange(g[[1]],g[[2]],g[[3]],g[[4]],ncol=2)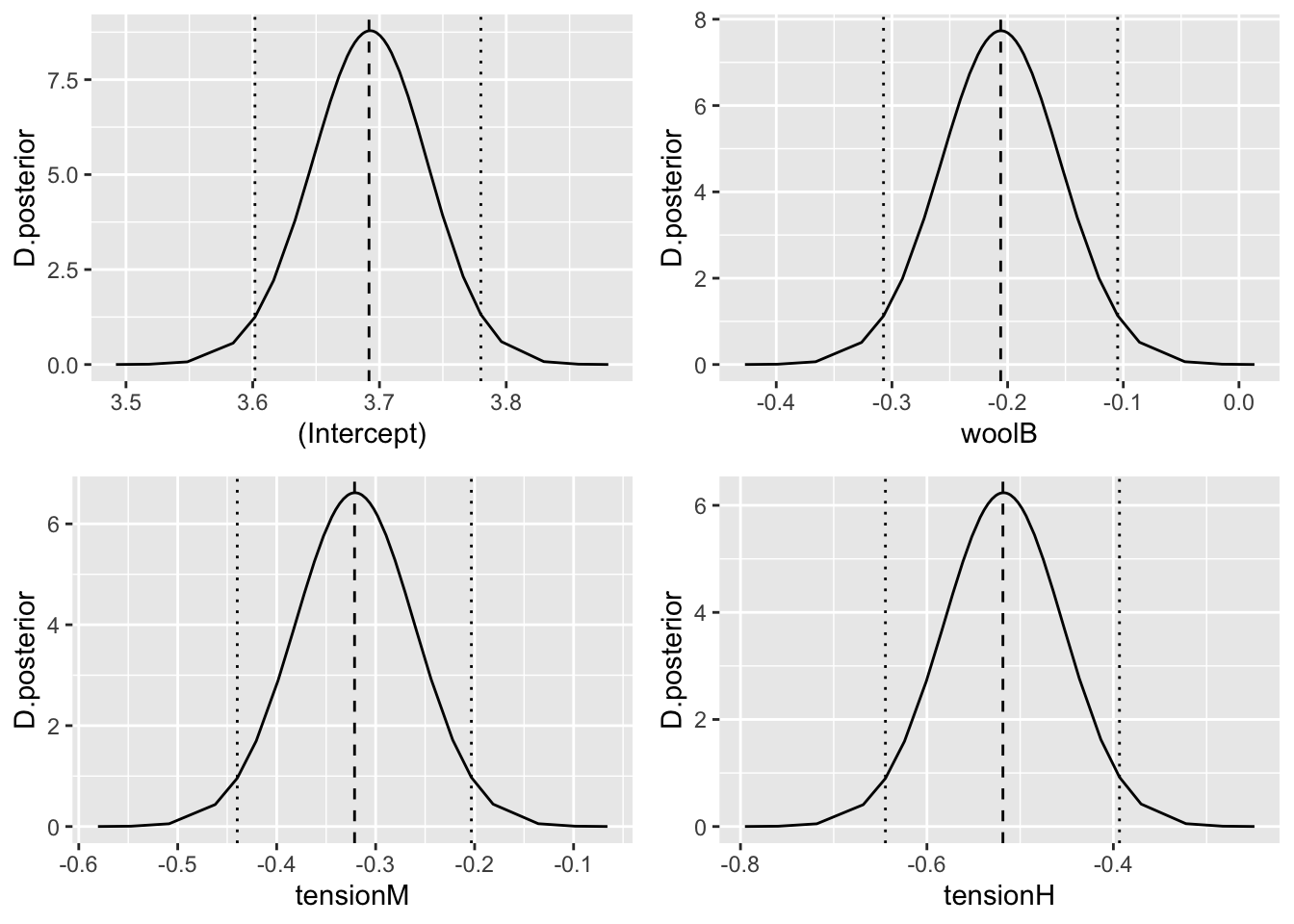

Figura 4.5: Distribución posterior de los efectos fijos

Y si queremos intentar una interpretación en términos de exponenciales de los efectos, tenemos sus distribuciones posteriores representadas en la Figura 4.6.

fixed=names(fit$marginals.fixed)
g=list()
for(i in 1:length(fixed)){
  exp.eff=inla.tmarginal(function(x) exp(x),fit$marginals.fixed[[i]])
  g[[i]]=ggplot(as.data.frame(exp.eff),aes(x=x,y=y))+
    geom_line()+
    geom_vline(
      xintercept=inla.emarginal(function(x) exp(x),
                 fit$marginals.fixed[[i]]),
               linetype="dashed")+
    geom_vline(xintercept=inla.hpdmarginal(0.95,exp.eff),
               linetype="dotted")+
    labs(x=fixed[i],y="D.posterior")
}
grid.arrange(g[[1]],g[[2]],g[[3]],g[[4]],ncol=2)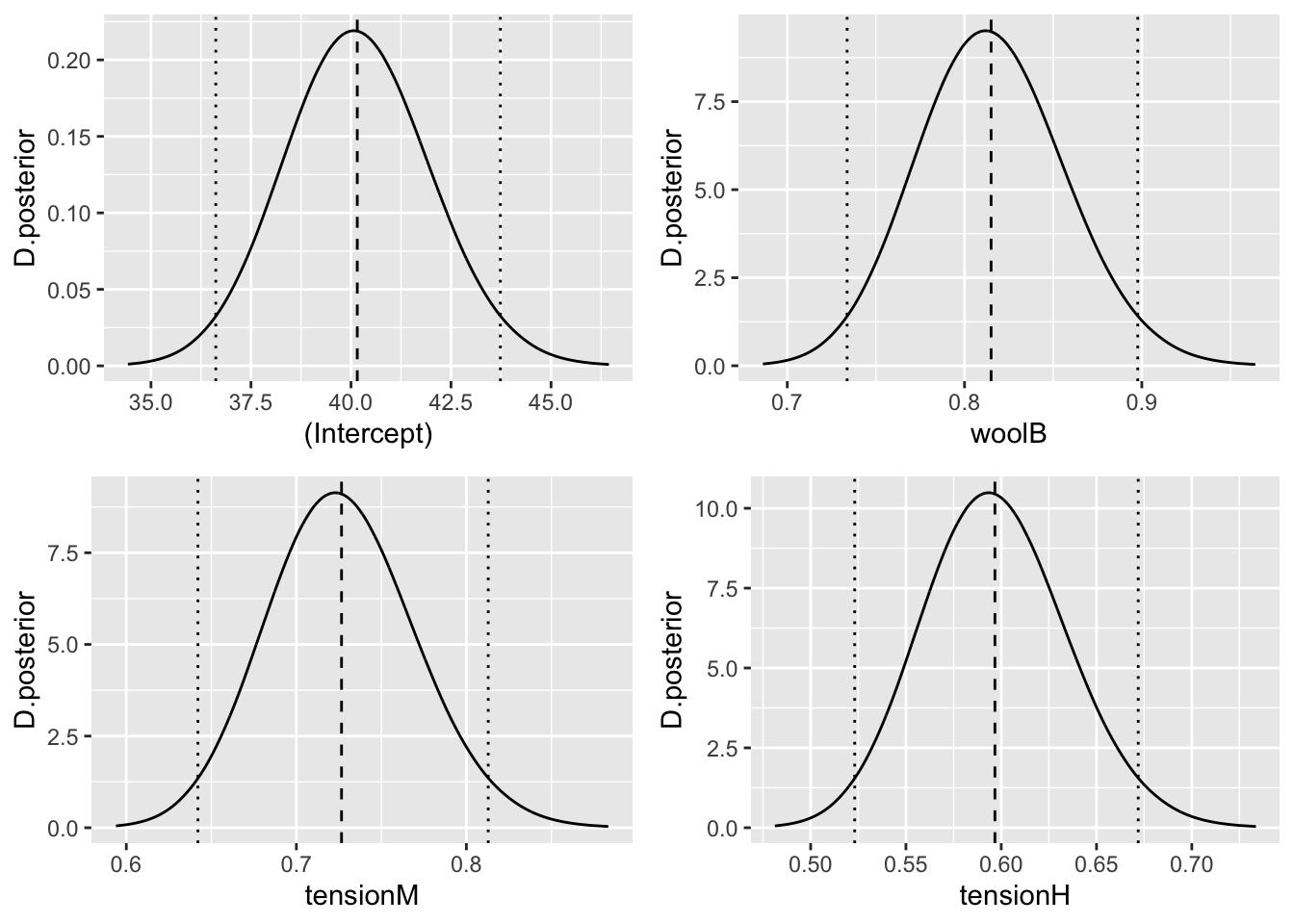

Figura 4.6: Distribución posterior de los exponenciales de los efectos fijos

Si quisiéramos reajustar el modelo utilizando como nivel de referencia en la variable tension el nivel H y en wool el nivel B, lo hacemos con la función relevel.

warp=warpbreaks %>%
  mutate(wool=relevel(wool,"B"),
         tension=relevel(tension,"H"))
formula= breaks ~ wool + tension
fit=inla(formula,family="poisson",data=warp,
         control.compute=list(return.marginals.predictor=TRUE))

Y obtenemos entonces las distribuciones posteriores para los exponenciales de los efectos fijos, en la Figura 4.7.

fixed=names(fit$marginals.fixed)
g=list()
for(i in 1:length(fixed)){
  exp.eff=inla.tmarginal(function(x) exp(x),fit$marginals.fixed[[i]])
  g[[i]]=ggplot(as.data.frame(exp.eff),aes(x=x,y=y))+
    geom_line()+
    geom_vline(
      xintercept=inla.emarginal(function(x) exp(x),
                 fit$marginals.fixed[[i]]),
               linetype="dashed")+
    geom_vline(xintercept=inla.hpdmarginal(0.95,exp.eff),
               linetype="dotted")+
    labs(x=fixed[i],y="D.posterior")
}
grid.arrange(g[[1]],g[[2]],g[[3]],g[[4]],ncol=2)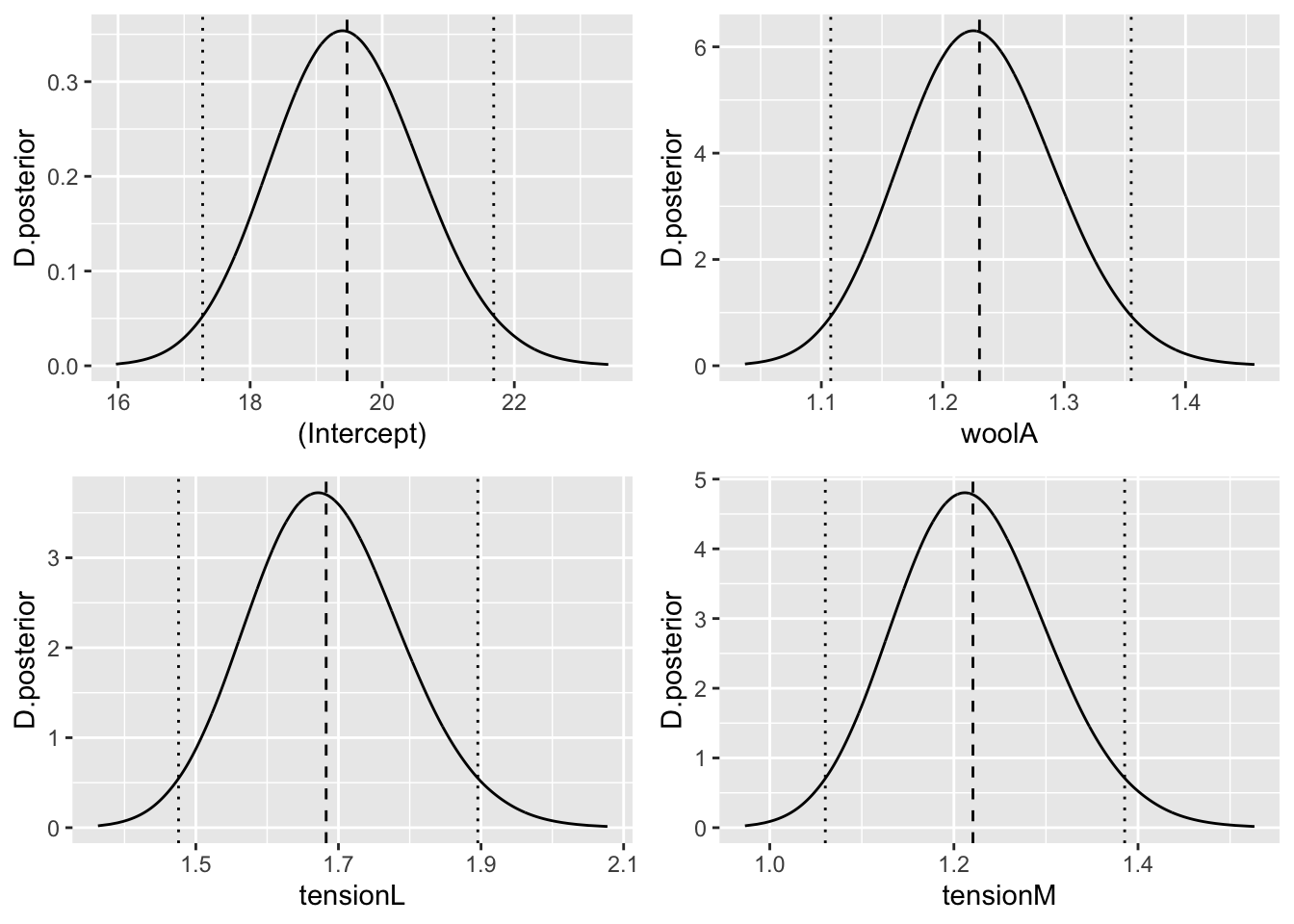

Figura 4.7: Distribución posterior de los exponenciales de los efectos fijos, con niveles de referencia wool=B y tension=H

4.3.2 Incidentes en barcos

Utilizamos los datos ShipsIncidents en datasets for SSTM-RINLA para estimar el riesgo mensual de incidentes en barcos. Los factores potenciales del riesgo son el periodo de construcción (built), el periodo de operación (oper) y el tipo de barco (type).

El modelo se formula considerando que el número de incidentes será proporcional al número de meses que ha navegado el barco, de modo que utilizaremos como offset el log(months), donde months son los meses que ha navegado el barco y que ponderan en consecuencia el riesgo de incidentes $\rho=\lambda/months$.

El modelo con el offset será entonces \[y_{ijkl} \sim Poisson (\lambda_{ijkl} )\\ \eta_{ijkl}=log(\lambda_{ijkl})= \theta + \alpha_i^b+\alpha_j^o+\alpha_k^t+Offset(log(month)_{ijkl})\]

Para los efectos fijos especificaremos las distribuciones a priori por defecto que proporciona INLA.

url="https://raw.githubusercontent.com/BayesModel/data/main/Ships.csv"
ShipsIncidents <- read.csv(url,sep=",") 

formula.inla <- y ~ 1 + built + oper + type
fit <- inla(formula.inla,family="poisson", 
            data=ShipsIncidents, offset=log(months),
            control.compute=list(return.marginals.predictor=TRUE))
round(fit$summary.fixed[,1:5],3)
#>               mean    sd 0.025quant 0.5quant 0.975quant
#> (Intercept) -6.416 0.217     -6.852   -6.413     -5.998
#> built65-69   0.696 0.150      0.406    0.695      0.994
#> built70-74   0.819 0.170      0.487    0.818      1.153
#> built75-79   0.453 0.233     -0.012    0.455      0.903
#> oper75-79    0.384 0.118      0.153    0.384      0.617
#> typeB       -0.543 0.178     -0.882   -0.546     -0.185
#> typeC       -0.688 0.329     -1.366   -0.678     -0.075
#> typeD       -0.075 0.291     -0.664   -0.069      0.476
#> typeE        0.326 0.236     -0.141    0.327      0.785

Vamos pues a interpretar algunos de los efectos fijos. El parámetro $exp(\theta)$ representa el ratio medio de incidentes por mes navegado para los barcos que fueron construidos entre el 60 y el 64, han operado entre el 60 y el 74 y son de tipo A (las categorías de referencia). El parámetro $exp(\alpha_E^t)$ proporciona el incremento respecto de la categoría base type=A que se produce en el ratio mensual de incidentes en los barcos de type=E. Las distribuciones posteriores de dichos efectos se muestra en la Figura 4.8.

#names(fit$marginals.fixed)
# ratio medio de incidentes por mes en las categorías base
rbase=inla.tmarginal(function(x) exp(x),fit$marginals.fixed[[1]])
# riesgo relativo de barcos tipo E
riesgoE=inla.tmarginal(function(x) exp(x),fit$marginals.fixed$typeE)

g1=ggplot(as.data.frame(rbase),aes(x=x,y=y))+
  geom_line()+labs(x="Riesgo base=incidentes por mes",y="D.Posterior")
g2=ggplot(as.data.frame(riesgoE),aes(x=x,y=y))+
  geom_line()+labs(x="Riesgo relativo type=E-A",y="D.Posterior")
grid.arrange(g1,g2,ncol=2)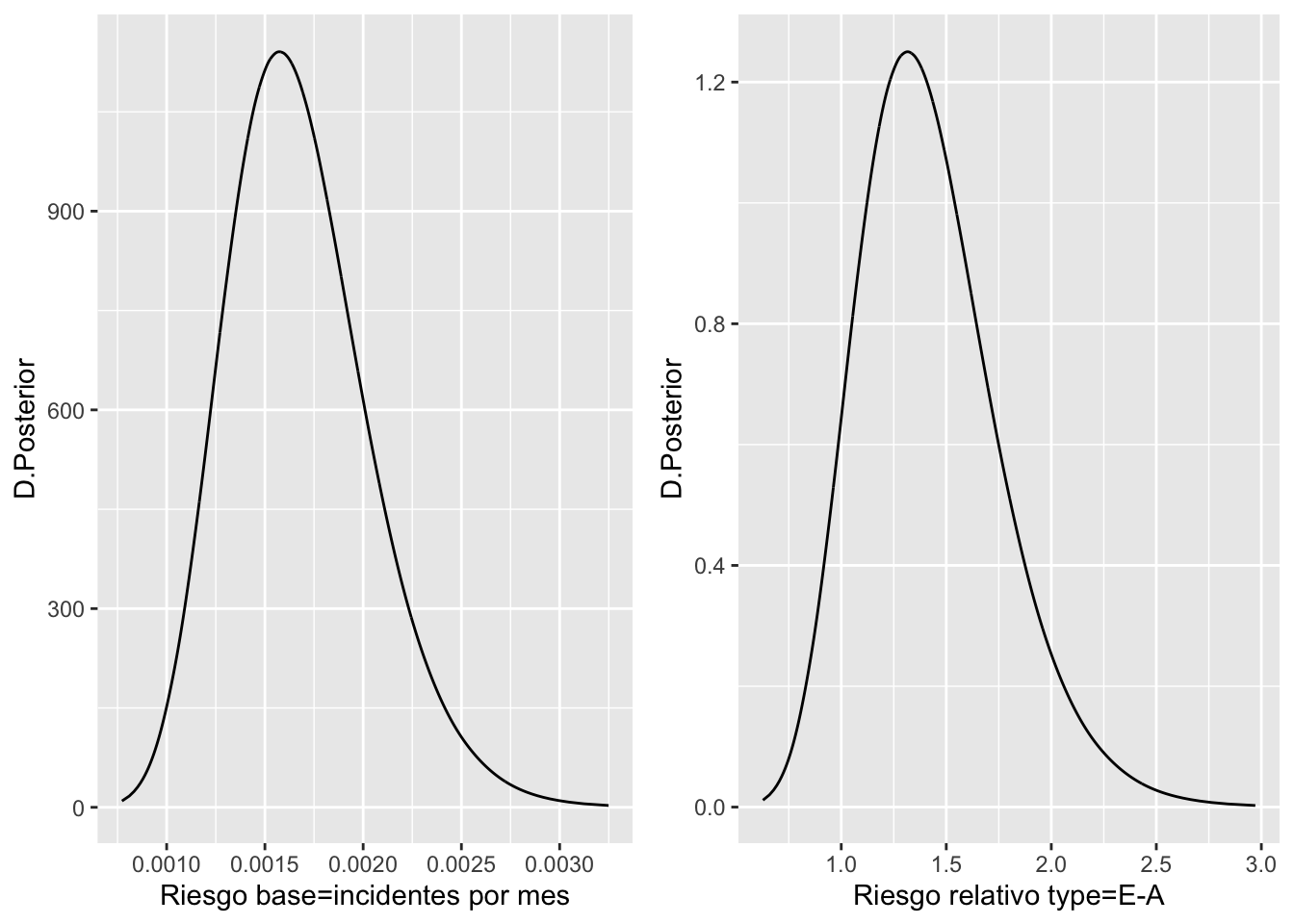

Figura 4.8: Distribuciones posteriores de los coeficientes relativos al riesgo base e incremento relativo por tipo E

Para el riesgo base tenemos:

# descriptivos
des.rbase=inla.zmarginal(rbase)
#> Mean            0.00167376 
#> Stdev           0.000362092 
#> Quantile  0.025 0.00105947 
#> Quantile  0.25  0.00141477 
#> Quantile  0.5   0.00163997 
#> Quantile  0.75  0.00189552 
#> Quantile  0.975 0.0024769

esto es, el ratio de incidentes por cada 1000 meses navegados por barcos en los niveles base de todos los factores, es decir, fabricados antes del 65, con periodo de operación 60-74 y de tipo A, será de 1.67 incidentes.

Para el incremento del riesgo de los barcos de tipo E respecto de los de tipo A, sin variar el resto de condiciones en los niveles base (construidos antes del 64 y con periodo de operación 60-74), tenemos:

des.riesgoE=inla.zmarginal(riesgoE)
#> Mean            1.42397 
#> Stdev           0.336616 
#> Quantile  0.025 0.870054 
#> Quantile  0.25  1.18227 
#> Quantile  0.5   1.38686 
#> Quantile  0.75  1.62474 
#> Quantile  0.975 2.18636

es decir, el riesgo de incidente por usar un barco de tipo E respecto a usar uno de tipo A se incrementa en un 42.4%.

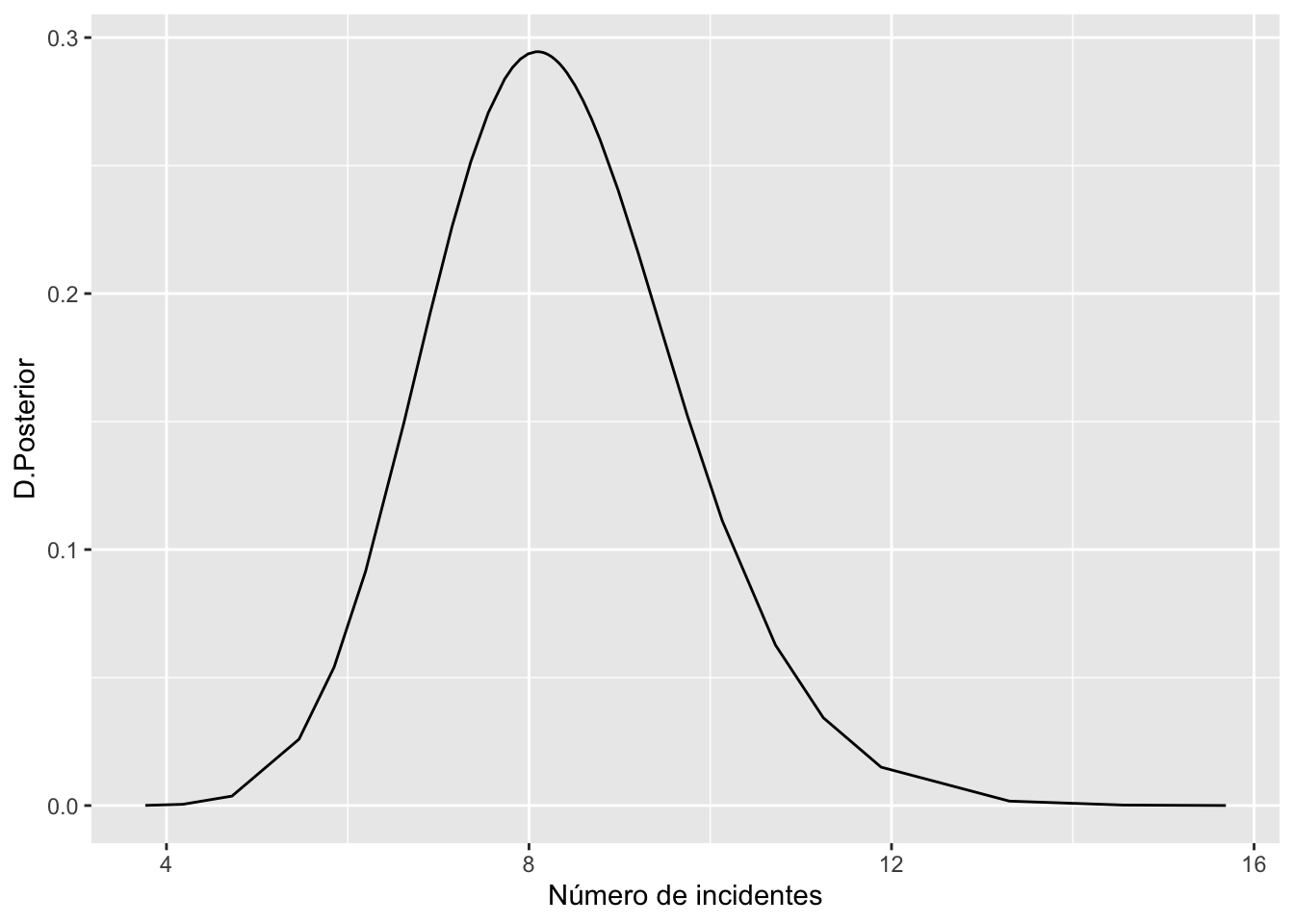
La distribución posterior para un barco de tipo A, construido entre los años 70-74 y con periodo de operación 75-79 y funcionando 1500 meses, viene dada en la Figura ??.

formula <- y ~ 1 + built + oper + type
new.data <- data.frame(type="A",
                       built ="70-74", 
                       oper = "75-79",
                       months=1500,
                       y=NA,
                       id=NA)
ships.combinado <- rbind(ShipsIncidents,new.data) 

## creamos un vector con NA's para observaciones y 1's para predicciones
ships.indicador <- c(rep(NA, nrow(ShipsIncidents)), 1)
## reajustamos el modelo añadiendo la opción de predicción de datos
fit.pred <- inla(formula, family="poisson",data = ships.combinado, 
                 offset=log(months),
                 control.compute=list(return.marginals.predictor=TRUE),
                 control.predictor = list(link = ships.indicador))
## y describimos los valores ajustados para los tres escenarios añadidos
fit.pred$summary.fitted.values[nrow(ships.combinado),]
#>                         mean      sd 0.025quant 0.5quant
#> fitted.Predictor.35 8.324152 1.37842   5.849265 8.246215
#>                     0.975quant mode
#> fitted.Predictor.35     11.247   NA
pred=fit.pred$marginals.fitted.values[[nrow(ships.combinado)]]
ggplot(as.data.frame(pred),aes(x=x,y=y))+
  geom_line()+
  labs(x="Número de incidentes",y="D.Posterior")

3 Modelo de ANOVA

Referencias